SOMMARIO: In attesa dell’imminente pronuncia delle Sezioni Unite, l’articolo si concentra sulle principali problematiche che caratterizzano l’operatività dei mutui con ammortamento alla francese. L’approccio metodologico condotto nelle pagine del presente contributo concilia l’analisi giuridica delle maggiori criticità legate al tema in esame con gli studi di matematica finanziaria. Sulla base di simili premesse teoriche, pertanto, vengono approfonditi alcuni aspetti di rilievo primario relativi a una forma di finanziamento rappresentante un modello negoziale tipico: dall’esclusione della violazione della disciplina dell’art. 1283 c.c., al tempo e alle modalità di pagamento degli interessi, fino al costo del finanziamento e alle sue modalità di calcolo.
ABSTRACT: In anticipation of the imminent ruling by the Grand Chamber of the Italian Supreme Court, this article focuses on the main issues characterizing the functionality of compound interest amortization plan (so called “Piano di ammortamento alla francese”). The methodological approach undertaken in this contribution reconciles the legal analysis of the major issues related to the subject with studies in financial mathematics. Based on similar theoretical premises, some aspects of primary relevance related to a typical negotiated financing model are explored: from the exclusion of the violation of Article 1283 of the Civil Code, to the timing and methods of interest payment, up to the cost of financing and its calculation methods.
1. Il rinvio pregiudiziale.
La recente ordinanza del tribunale di Salerno del 19.07.23[1] di rinvio pregiudiziale alla corte di cassazione ex art. 363 bis c.p.c. costituisce l’occasione per riesaminare questioni che da tempo sono state sollevate sulla legittimità del mutuo con ammortamento c.d. alla francese, sotto diversi aspetti: la violazione del divieto di anatocismo di cui all’art. 1283 c.c.; l’indeterminatezza o indeterminabilità dell’oggetto del contratto ex art. 1346 c.c.; l’indeterminatezza del tasso di interesse ex art. 1284 comma 3 c.c.; l’indeterminatezza del tasso di interesse e delle condizioni contrattuali ex art. 117 comma 4 Testo Unico Bancario; la violazione delle regole di trasparenza bancaria.
Il giudizio a quo, secondo quanto esposto in premessa nell’ordinanza del tribunale, ha per oggetto un mutuo ipotecario recante l’indicazione del numero delle rate da restituire, del loro ammontare, del Tasso Annuo Nominale, del Tasso Annuo Effettivo, al quale è allegato un piano di ammortamento a rate costanti, che riporta la composizione in quota capitale ed in quota interessi di tutte le rate, ed il loro ammontare totale.
La motivazione dell’ordinanza ripropone temi ricorrenti nel dibattito giurisprudenziale e dottrinale, quali la maggiore onerosità dell’ammortamento alla francese rispetto all’ammortamento all’italiana, la qualificazione come condizione contrattuale della formula matematica utilizzata per il calcolo della rata, la maggiore gravosità del tasso effettivo rispetto a quello dichiarato nel contratto, l’anticipazione del pagamento degli interessi rispetto alla restituzione del capitale, l’individuazione nell’art. 821 comma 3 c.c. dell’opzione normativa per la capitalizzazione semplice degli interessi.
Il tribunale ha sollevato la questione in questi termini: “Dica la Corte di Cassazione se la mancata indicazione della modalità di ammortamento c.d. “alla francese” e/o del regime di capitalizzazione “composto” degli interessi passivi all’interno di un contratto di mutuo bancario stipulato nella vigenza del Decreto Legislativo n. 385 del 1993, anche per il caso in cui la modalità c.d. “alla francese” ed il regime di capitalizzazione “composto” siano desumibili dal cliente facendo ricorso al complesso delle condizioni contrattuali ed economiche pattuite (comprese quelle contenute nel piano di ammortamento allegato al contratto) integri oppure no un’ipotesi di nullità parziale del contratto di mutuo bancario ai sensi dell’articolo 117, comma 4, del D.Lgs. n. 385/1993, con le conseguenze di cui al comma 7 della succitata disposizione”.
Il giudice remittente infatti ha individuato nel mutuo sottoposto al suo esame due aspetti problematici, che espressamente qualifica come distinti, come tali suscettibili di presentarsi separatamente o congiuntamente: la mancata indicazione della modalità di ammortamento c.d. “alla francese”, quale specifica modalità con cui vengono composte, in capitali ed interessi, le singole rate del prestito, e la mancata indicazione del regime di capitalizzazione composta, secondo il quale gli interessi si sommano al capitale e producono nuovi interessi.
L’ordinanza non specifica se l’indicazione della modalità di ammortamento, che assume sia mancante, possa essere data semplicemente con l’utilizzo dell’espressione “ammortamento alla francese”, che in questo caso si dovrebbe ritenere per sé stessa compiutamente indicativa dei criteri adottati per la stesura del piano di ammortamento, o se si richieda una formulazione più dettagliata, ed eventualmente quale. Contiene però una definizione del piano di ammortamento alla francese, come quello caratterizzato dalla “corresponsione di rate costanti in cui la quota parte degli interessi è progressivamente decrescente e quella della sorte capitale crescente, in cui vengono cioè ad essere corrisposti dapprima prevalentemente gli interessi e poi il capitale”.
Sul secondo aspetto, l’adozione del regime di capitalizzazione composta, l’ordinanza sostiene, richiamando gli articoli 3 e 6 della Delibera del C.I.C.R. del 9 febbraio 2000, applicabile ratione temporis, che questa non era in assoluto preclusa, e che la sua mancata indicazione rileverebbe non sotto il profilo della violazione del divieto di anatocismo, non dedotta in giudizio, ma sotto il profilo della determinatezza/determinabilità dell’oggetto del contratto e del rispetto della trasparenza bancaria. A questo proposito pare di dovere osservare che la regola generale rimane quella del divieto di anatocismo e che le uniche eccezioni riferibili al mutuo previste dalla delibera citata riguardano gli interessi moratori (art. 3 comma 1 e 2) e di pre-ammortamento (art. 3 comma 4) ma non gli interessi ricompresi nelle rate; sicché l’esistenza di interessi che si sommano al capitale e producono interessi, indicata nell’ordinanza come insita nel regime di capitalizzazione composta, dovrebbe per sé stessa essere reputata illecita e non dovrebbe poter essere sanata dalla espressa indicazione di tale regime nel contratto.
La questione sollevata, superato il vaglio preliminare di ammissibilità della prima presidente, è stata assegnata alle sezioni unite.
2. Un modello negoziale “tipico”.
Il mutuo con ammortamento alla francese è un modello negoziale che presenta nella prassi dei caratteri ben definiti e costanti, da lungo tempo individuati dalla dottrina matematico-finanziaria:
1) il capitale mutuato al momento iniziale del finanziamento è restituito progressivamente, in rate di importo costante e di numero e periodicità (ad esempio, mensile, semestrale, annuale) predefinite;
2) ogni rata è costituita da una quota interessi e da una quota capitale;
3) la somma delle quote capitale delle singole rate corrisponde all’importo totale del prestito e di conseguenza il pagamento dell’ultima rata estingue il finanziamento;
4) con il pagamento della prima rata vengono pagati tutti gli interessi maturati nel primo periodo sul capitale mutuato e col pagamento delle rate successive tutti gli interessi maturati sul capitale residuo nel periodo di riferimento di ciascuna rata (ad esempio col pagamento della seconda rata mensile vengono pagati gli interessi maturati nel secondo mese);
5) la quota capitale di ciascuna rata è pari alla differenza fra il suo importo totale e la quota interessi.
Precisiamo che per ora intendiamo questi caratteri come elementi strutturali e non come condizioni contrattuali; la precisazione è necessaria perché alcune delle questioni sollevate riguardano il se ed il come essi trovino riscontro nelle pattuizioni negoziali.
Precisiamo anche che non intendiamo, enunciandoli, precostituire in modo tautologico la soluzione di alcuna questione giuridica, ma solo riconoscere come si presenta nella realtà operativa l’oggetto dell’analisi; infatti vi è un consenso diffuso sull’esistenza nella prassi negoziale di un modello, che potremmo definire tipico, di comune applicazione, che li riproduce costantemente[2], anche da parte di quegli studiosi che adottano una posizione critica, ed anche in relazione alla condizione n. 4, che è quella di più evidente rilevanza rispetto al tema dell’anatocismo.
Si tratta dunque di una mera constatazione di fatto, la cui fondatezza non è scalfita dal carattere meramente empirico e genericamente descrittivo di molte definizioni correnti, in particolare di quelle che ne individuano gli elementi caratterizzanti semplicemente nella costanza della rata e nella sua composizione di una quota di interessi decrescente nel tempo e di una quota di capitale crescente, né dalla astratta ammissibilità, dal punto di vista della scienza finanziaria, di modalità alternative di costruzione dell’ammortamento a rata costante.
Certo però l’esame delle obiezioni che da tempo vengono sollevate nella dottrina giuridica e nella letteratura matematico finanziaria, recepite da una parte minoritaria della giurisprudenza di merito, deve essere condotto primariamente con riferimento alla figura così definita ed a questa quindi faremo riferimento, ove non sia diversamente indicato, con l’espressione “ammortamento alla francese”.
Infine, precisiamo che la nostra analisi sarà limitata all’ipotesi di mutuo a tasso fisso per tutta la durata del finanziamento e che quindi le peculiari questioni che si pongono nell’ipotesi di previsione di un tasso di interesse variabile non saranno oggetto di esame.
3. L’anatocismo ed il costo occulti.
La prevalente giurisprudenza di merito[3] sinora si è pronunciata per l’insussistenza dei profili di illegittimità denunciati, sulla base di considerazioni che appaiono direttamente conseguenti alle caratteristiche della fattispecie, sopra delineate.
Si esclude la violazione dell’art. 1283 c.c., rilevando che gli interessi maturati a ciascuna scadenza sono corrisposti come componenti della rata di riferimento, che ciascun pagamento periodico esaurisce la totalità degli interessi sino a quel momento maturati, che gli interessi dovuti in ogni rata successiva sono calcolati sul debito residuo per sorte capitale, progressivamente ridotto per effetto del pagamento della quota capitale delle rate precedenti, e quindi che difetta il presupposto essenziale dell’anatocismo, l’applicazione di interessi su interessi già maturati, e che infatti si riscontra non l’aumento ma la riduzione nel tempo della loro base di calcolo[4].
Sotto il profilo della determinatezza dell’oggetto del contratto si afferma che le condizioni negoziali contengono tutti gli elementi necessari e sufficienti per la costruzione del piano di ammortamento, e che non sussiste alcuna discrezionalità dell’intermediario nella quantificazione del proprio credito.
Si aggiunge sovente la considerazione che il criterio di restituzione del debito che privilegia, sotto il profilo cronologico, l’imputazione agli interessi piuttosto che al capitale – in virtù del quale la quota interessi delle prime rate è elevata e si riduce solo gradualmente, determinando un allungamento del rimborso del capitale – appare conforme al disposto dell’art. 1194 c.c., secondo il quale il pagamento deve essere prioritariamente imputato agli interessi scaduti.
Le contestazioni sollevate nei confronti di queste conclusioni imputano loro il travisamento della realtà del fenomeno e la patente contraddizione con le conclusioni della matematica finanziaria.
Poiché siamo sul crinale fra matematica finanziaria e diritto, si pone il problema di come tradurre e qualificare in termini giuridici concetti e conclusioni proprie dell’ambito matematico e di stabilire quale rilevanza debbano assumere in ambito giuridico. Se il ricorso alla matematica finanziaria appare essenziale per la comprensione del fenomeno e delle sue dinamiche, compete pur sempre al diritto definire e qualificare il proprio oggetto di disciplina e determinare i presupposti applicativi delle norme giuridiche; di conseguenza quando si fa riferimento a concetti tratti dalla matematica finanziaria è necessario esplicitare il loro riferimento normativo ed individuare il loro profilo giuridicamente rilevante, onde evitare l’impropria invocazione dell’autorità, su questioni eminentemente di diritto, di conclusioni che si assumono scientificamente fondate in un altro ambito del sapere.
Secondo una corrente di pensiero[5] che ha origine nella letteratura matematico-finanziaria ed è seguita da alcune decisioni di merito la corrispondenza della quota interessi della singola rata al prodotto fra il tasso contrattuale, normalmente qualificato in contratto come T.A.N. (Tasso Annuo Nominale), ed il capitale residuo non esclude che si sia in presenza di un fenomeno riconducibile all’anatocismo, quanto meno sotto un profilo sostanziale: questo perché, pur rilevandosi apparentemente l’impiego del regime semplice nella determinazione della quota interessi, l’importo complessivo della rata sarebbe maggiorato in virtù della applicazione del TAN in regime di capitalizzazione composta e già includerebbe, “per costruzione”, interessi anatocistici.
In questa ricostruzione assumono particolare rilievo l’anticipazione del pagamento degli interessi maturati rispetto alla scadenza dell’obbligazione restitutoria del capitale residuo, sul quale essi sono calcolati, la maggiorazione del debito residuo conseguente al calcolo della rata in regime di capitalizzazione composta, la ripartizione della rata in quota capitale e quota interessi.
Sotto il primo aspetto si afferma che l’anticipazione del pagamento degli interessi presuppone una fittizia chiusura anticipata del finanziamento – in contrasto con il principio per cui l’obbligazione restitutoria, per quanto frazionata in fase esecutiva, ha carattere unitario – al fine di riscuotere anticipatamente gli interessi maturati con la rata in scadenza, con contestuale roll over (proroga) degli altri rimborsi e sostanziale elusione dell’art. 1283 c.c.
Sotto il secondo aspetto si rileva che il debito residuo è funzione della quota capitale delle rate precedenti che, a sua volta, dipende dal calcolo della rata costante, che è eseguito in regime di capitalizzazione composta.
Sotto il terzo aspetto si osserva che l’ammortamento alla francese posticipa, mediante l’imputazione ad interessi di una quota della rata, per un ammontare corrispondente all’importo di tale quota, il pagamento del capitale, così che gli interessi sarebbero calcolati su un capitale residuo che sconta l’imputazione a pagamento del capitale non dell’intera rata precedente ma della sola quota capitale.
Si conclude che l’applicazione del regime di capitalizzazione composta introduce in modo occulto, mediante l’applicazione del fattore esponenziale proprio della relativa formula matematica, un meccanismo di calcolo di interessi sugli interessi, e che gli interessi distribuiti in ciascuna rata sono in rapporto di dipendenza proporzionale rispetto a quelli compresi nelle rate pregresse, pur se formalmente pagati alle rispettive scadenze, con conseguente maggiorazione dell’ammontare complessivo degli interessi e del costo del mutuo.
Dal punto di vista giuridico sono state proposte diverse qualificazioni della fattispecie negoziale che si assumono coerenti con queste argomentazioni:
- nullità parziale per violazione del divieto di anatocismo ex art. 1283 c.c., eventualmente con l’interposizione dell’art. 1344 c.c.;
- difformità fra il contenuto dispositivo del contratto e la sua esecuzione da parte dell’intermediario, in virtù della mancata indicazione nel testo contrattuale della formula utilizzata per il calcolo della rata e/o della applicazione di un tasso effettivo superiore a quello indicato (qualora non si ravvisi anatocismo in senso giuridico);
- indeterminatezza del tasso di interesse ex artt. 1284 comma 3 c.c. e 117 comma 4 Testo Unico Bancario.
Mentre nella prima e nella seconda ipotesi la conseguenza dovrebbe essere la sostituzione del piano di ammortamento con quello in interesse semplice o con quello individuato come conforme alle pattuizioni contrattuali, nella terza ipotesi si dovrebbe anche procedere all’applicazione del tasso sostitutivo previsto dalla legge in luogo del tasso indicato nel contratto.
In effetti si deve rilevare che gli interessi dal punto di vista matematico appaiono maggiorati rispetto all’ipotesi di integrale imputazione della rata a pagamento del capitale, perché la loro base di calcolo include una frazione del capitale residuo pari alle quote delle rate precedenti che, invece di essere imputate a restituzione del capitale, sono state imputate alla prestazione accessoria[6].
Ad esempio la quota interessi della seconda rata è calcolata non sulla differenza fra il capitale erogato e la prima rata ma sulla differenza fra il capitale erogato e la sola quota capitale di questa, ed in questo senso su una base di calcolo “maggiorata” dell’importo della quota interessi della rata iniziale; “maggiorazione” che determina un corrispondente aumento della quota interessi della rata successiva, che effettivamente corrisponde matematicamente all’applicazione del TAN sulla quota interessi della rata precedente.
In altri termini la quota interessi della rata n-esima In, che è uguale al prodotto fra il tasso di interesse[7] i ed il capitale residuo, può essere espressa nella forma
In = i (D – C)
dove D è il capitale mutuato e C la somma delle quote capitale delle rate precedenti;
ora, poiché la somma delle quote capitale è pari all’importo totale delle rate anteriori, R, meno la somma delle relative quote interessi, I, abbiamo
C = R – I
e quindi
In = i [D – (R – I)]
che diventa
In = iD – iR + iI
dove fra le componenti della quota interessi della rata figura il prodotto fra il tasso di interesse e gli interessi corrisposti nelle rate precedenti.
Poiché questo è vero per ogni rata successiva alla prima, ad ogni scadenza si verificherebbe la produzione di interessi sugli interessi inglobati nelle rate precedenti, anche se già pagati, con correlativa progressione geometrica del loro importo, in quella che viene definita una “spirale ascendente” di produzione di interessi su interessi.
Ma se compare, preceduto dal segno positivo, il prodotto iI, è solo perché si è scelto di determinare il capitale residuo sottraendo dal capitale iniziale non la quota capitale di ogni singola rata ma il suo intero importo, comprensivo della quota interessi, per poi riaggiungerla: “ogni debito residuo risultante dal pagamento delle rate già versate si ottiene sottraendo dal debito precedente (quale risultante dal pagamento della rata immediatamente anteriore) la quota capitale corrente (quella che compone la rata che si prende in considerazione), vale a dire “sottraendo (contabilizzando) la rata ed aggiungendo (capitalizzando) la quota interessi, la quale verrà quindi considerata nel calcolo delle successive quote interessi”[8].
Ci sembra però che la questione dovrebbe essere semplicemente se la quota interessi sia individuata e quantificata correttamente; in caso affermativo la sua imputazione, appunto, al pagamento degli interessi e non alla restituzione del capitale risulterebbe ovvia, ed ovvia e corretta la conseguenza, che non possa essere detratta dal debito.
Riconducendo il discorso sui binari del diritto, si impone l’esame delle seguenti questioni:
se sia ammissibile il pagamento alla scadenza di ogni rata degli interessi maturati sull’intero capitale residuo, e se sia propriamente definibile come “anticipazione”;
quale sia il significato dell’utilizzo per il calcolo della rata di una formula in interesse composto, e quali le sue implicazioni;
che rapporto vi sia fra tasso di interesse, tempo di pagamento degli interessi, costo del finanziamento.
4. Il tempo del pagamento degli interessi.
Gli interessi del mutuo sono ricondotti tradizionalmente, unitamente agli interessi sul prezzo della cosa fruttifera consegnata prima che il prezzo divenga esigibile (art. 1499 c.c.) ed agli interessi che maturano sulle rimesse sul conto corrente ordinario (art. 1825 c.c.), alla categoria degli interessi compensativi[9], i quali costituiscono il compenso del godimento di un capitale attualmente non esigibile, e per questo si distinguono dagli interessi disciplinati dall’art. 1282 c.c., che maturano per effetto della scadenza del debito principale.
L’obbligazione di interessi riveste un ruolo essenziale nel sinallagma negoziale, e per questa ragione non è qualificabile come mera obbligazione accessoria rispetto a quella di restituzione del capitale[10]; al contrario essa soltanto ha carattere propriamente corrispettivo del godimento del capitale, mentre l’obbligazione restitutoria è correlativa all’esaurimento della durata e della funzione del contratto. In questo senso gli interessi del mutuo possono essere paragonati ai canoni di locazione e la restituzione del capitale alla riconsegna del bene locato, e certo difficilmente si potrebbe sostenere che il pagamento dei canoni abbia carattere accessorio rispetto alla riconsegna del bene o che i canoni non possano essere esigibili prima di essa.
La ragione della deroga alla previsione dell’art. 1282 c.c. è generalmente riconosciuta nella tutela dell’equilibrio economico tra i contraenti, in particolare nella necessità di attribuire al mutuante un compenso per il mancato godimento del capitale; così l’art. 1815 comma primo c.c., che prevede la naturale onerosità del mutuo, prescinde dall’esigibilità del capitale e si pone su un piano del tutto distinto rispetto all’art. 1282 c.c.
La naturale onerosità del mutuo fa sì che gli interessi maturino anche in assenza di pattuizione, quindi anche in assenza di indicazione nel contratto sia del tasso sia della base di calcolo: per il tasso soccorre l’art. 1284 c.c.; per la base di calcolo il senso della norma, e la sua autonomia rispetto all’art. 1282 c.c., impongono che essa sia costituita dall’intero capitale mutuato e non ancora restituito. Il pagamento degli interessi peraltro è previsto dall’art. 1820 c.c., a pena di risoluzione, in modo autonomo rispetto all’obbligo di restituzione del capitale. Anche la possibilità di restituzione rateale del capitale è espressamente prevista, dall’art. 1819 c.c., e quindi l’ipotesi che gli interessi maturino nel corso del rapporto su un ammontare variabile in funzione della progressione del rimborso del finanziamento si deve considerare del tutto fisiologica.
Si intende che una cosa è la maturazione altra l’esigibilità, che è rimessa alla volontà delle parti, che possono differirla sino al momento finale del finanziamento, come pure riferirla ad una determinata cadenza temporale (ad esempio mensile, semestrale, annuale). Su quale sia la scadenza degli interessi, in assenza di espressa previsione negoziale, si registrano in dottrina opinioni diverse. E’ stato sostenuto che coincida con la periodicità usata per computare gli interessi[11], che sia annuale[12], che sia immediata ex art. 1183 primo comma c.c.[13], ed anche che debba coincidere con la restituzione del capitale[14], ma quest’ultima opinione è minoritaria e non ci risulta sia mai stata proposta se non nel contesto della critica all’ammortamento alla francese.
L’opinione prevalente come si vede non è affatto contraria all’esigibilità di interessi maturati su un capitale non ancora esigibile, ma anzi la considera insita nella loro natura, ed in questo si conforma alla logica economica: la periodica esigibilità dell’obbligazione di interessi realizza il pieno equilibrio di posizioni, nel senso che ad ogni scadenza il mutuatario si trova ad avere goduto del capitale per tutto il tempo trascorso dall’inizio del rapporto ed il mutuante ad avere percepito tutti gli interessi maturati nel medesimo arco di tempo.
Si deve dunque ritenere che l’esigibilità degli interessi relativi a un capitale ancora non esigibile, alla scadenza di ogni singolo periodo di maturazione, sia per il diritto un’ipotesi assolutamente fisiologica. A questi interessi si riferisce l’art. 2948 n. 4 c.c. in tema di prescrizione breve, che ne fa il paradigma dell’obbligazione periodica.
Alla luce di queste considerazioni possiamo concludere che il pagamento degli interessi al termine del singolo periodo di maturazione, successivamente al godimento del capitale di cui costituiscono il corrispettivo, non costituisce in senso proprio “anticipazione”, non incide sull’equilibrio delle parti in modo estraneo alla logica ed alla funzione del rapporto, non è incompatibile con il carattere unitario dell’obbligazione di restituzione del capitale, non presuppone una chiusura anticipata del finanziamento. Nel prosieguo ci riferiremo a questi interessi, calcolati sul capitale residuo, come interessi “anticipati”, con la precisazione, che formuliamo qui una volta per tutte, che tali sono rispetto alla restituzione del capitale ma non alla loro maturazione.
Queste conclusioni prescindono dalla disciplina dell’imputazione del pagamento dettata dall’art. 1194 c.c. Infatti questa disciplina presuppone l’esistenza al momento del pagamento di più debiti esigibili[15], mentre la composizione della rata è una questione logicamente anteriore che riguarda la determinazione dell’obbligazione contrattuale; così una volta che si sia stabilito che la rata è stata correttamente determinata secondo le previsioni del contratto, e nel rispetto delle norme cogenti applicabili, di fronte ad un pagamento pari al suo importo non vi sarebbe modo di sollevare alcun problema di imputazione, ed il pagamento dovrebbe essere imputato a restituzione del capitale ed a pagamento di interessi nelle misure desumibili dalle previsioni negoziali. Solo in presenza di un pagamento che non estingua interamente il debito, l’art. 1194 c.c. afferma il principio secondo cui deve essere imputato prima agli interessi ed alle spese, poi al capitale; si tratta di un criterio legale di imputazione che opera come limite diretto al potere d’imputazione del debitore previsto dall’art. 1193 c.c., cui consegue l’inefficacia dell’atto di imputazione nella parte in cui dà la precedenza al capitale rispetto agli interessi e alle spese[16]; tanto meno il debitore potrebbe pretendere di imputare il pagamento ad un capitale non ancora scaduto, essendo il relativo termine di pagamento stabilito anche nell’interesse del creditore (art. 1816 c.c.).
5. La rata in interesse composto.
La corrispondenza delle rate dell’ammortamento alla francese ad una formula matematica in interesse composto è un dato pacifico in matematica finanziaria[17]. L’importanza di questo punto è evidente da quelle decisioni che, sulla sola base del rilievo da parte del consulente tecnico d’ufficio del calcolo della rata in regime composto, ritengono senz’altro superata o irrilevante l’obiezione secondo cui la quota interessi può essere espressa in regime semplice. L’utilizzo di una formula in interesse composto per determinare il valore della rata costante e l’applicazione, nella medesima rata, di interessi in regime semplice sembrano incompatibili.
Infatti è affermazione ricorrente che se la rata è calcolata secondo una formula in interesse composto anche gli interessi in essa ricompresi necessariamente si devono ritenere calcolati in regime composto[18]; altra affermazione ricorrente è che se anche la formula in interesse composto non comportasse l’applicazione di interessi anatocistici comunque determinerebbe un importo maggiore della rata ed un aggravamento della posizione del debitore non previsto dal contratto.
È importante però esplicitare due condizioni immanenti all’utilizzo della formula, che sono anch’esse del tutto pacifiche in matematica finanziaria.
La prima è che essa produce un risultato conforme alla condizione del pagamento, ad ogni scadenza, di tutti gli interessi maturati in regime semplice nel periodo di riferimento, al tasso contrattuale, sul debito non ancora rimborsato, e che si tratta dell’unico valore della rata che soddisfi tale condizione[19].
A riprova di questo si può osservare che nelle ricostruzioni alternative dei piani di ammortamento in regime semplice proposte dai critici o che si possono vedere in qualche perizia stragiudiziale ed anche in qualche consulenza tecnica di ufficio, nelle quali la quota interessi è rideterminata ad un importo minore, detto importo rapportato al capitale residuo restituisce un tasso di interesse inferiore al tasso periodale desumibile dal TAN.
La seconda è che gli interessi composti evidenziati dalla formula presuppongono una ricomposizione delle rate (fermo restando l’importo di queste) nella quale la quota di capitale è rideterminata in misura pari al loro valore attualizzato in regime composto alla data iniziale del finanziamento[20], e la quota interessi corrisponde agli interessi sulla sola quota capitale così rideterminata calcolati, sempre in regime composto, dalla medesima data alla scadenza della rata.
In sostanza ogni rata viene considerata come un autonomo finanziamento con rimborso unico, di importo pari alla sua quota capitale, rideterminata nel modo descritto, che viene estinto col pagamento in unica soluzione, alla sua scadenza, del capitale e degli interessi maturati sino a tale momento, calcolati in regime composto, senza pagamenti intermedi[21].
Il complessivo piano di ammortamento è così riformulato – si intende, senza apportare alcuna variazione al numero, alla frequenza ed all’importo dei pagamenti – imputando in ciascuna rata i soli interessi relativi alla quota capitale, ma calcolati, al medesimo tasso, in regime composto, ed invertendone l’ordine. In pratica nella prima rata (esattamente corrispondente sia per importo sia per suddivisione fra quota capitale e quota interessi all’ultima rata dell’ammortamento alla francese) la quota capitale è preponderante e la quota interessi si riferisce ai soli interessi maturati su di essa sino alla sua scadenza, necessariamente semplici; a partire dalla seconda rata si considerano pagate una quota di capitale via via decrescente e gli interessi composti maturati sulla stessa (solo a partire dalla seconda rata ovviamente è configurabile l’anatocismo); nell’ultima rata (corrispondente alla prima dell’ammortamento alla francese) la quota capitale è al livello minimo e la quota interessi al livello massimo, perché comprende tutti gli interessi composti maturati su di essa per l’intera durata del finanziamento[22]. Non si ha più il pagamento ad ogni scadenza di tutti gli interessi di competenza dell’esercizio decorso, ma solo di quelli relativi al “sottoprestito” che si rimborsa, e così al debito per il capitale non ancora rimborsato si affianca un debito per interessi non pagati, che non è immediatamente esigibile ed è produttivo di ulteriori interessi[23].
Questa seconda puntualizzazione consente di risolvere quella che altrimenti sarebbe una evidente aporia dell’argomento basato sul calcolo della rata in regime di capitalizzazione composta: posto che il montante, pari alla somma delle rate, è dato, ed è data anche la somma delle quote di capitale, pari al capitale erogato, il complessivo monte interessi, determinato per differenza, necessariamente rimane invariato, e non si comprenderebbe come possa essere determinato sia in regime composto sia in regime semplice. Superata la contraddizione, si deve però riconoscere che siamo in presenza di un flusso monetario astrattamente ricostruibile come conforme a due diverse pattuizioni, dove se muta il regime degli interessi, da semplice a composto, muta anche la base di calcolo, e si dissolve la affermata incompatibilità fra determinazione della rata secondo una formula in interesse composto ed applicazione degli interessi in regime semplice.
Alla luce di questi rilievi riteniamo che l’argomento basato sull’utilizzo nel calcolo della rata di una formula in capitalizzazione composta sia tutt’altro che risolutivo. Si tratta, semplicemente, della prospettazione di una diversa ipotesi di composizione della rata, che non esclude affatto la sua corrispondenza all’interesse semplice, che al contrario si deve riconfermare.
In sostanza l’importo della rata è astrattamente conforme alla pattuizione dell’interesse semplice sul capitale residuo così come alla pattuizione dell’interesse composto sull’importo della rata attualizzato al momento iniziale.
Abbiamo così due flussi di cassa identici che possono essere il risultato di due pattuizioni diverse, una lecita e l’altra no.
La tesi che per questa ragione si debba ravvisare la violazione del divieto di anatocismo sostanzialmente presuppone che la pattuizione realmente applicata sia la seconda, per poi contestarne la legittimità.
Ma se il prestito, come avviene, è espresso in forma unitaria, in modo coerente con la realtà del fenomeno – poiché esprime la restituzione progressiva nel corso del tempo del capitale erogato e la maturazione degli interessi commisurati a tale capitale – davvero non riusciamo a vedere perché la sua legittimità non dovrebbe essere parametrata a tale ricostruzione, secondo la quale si richiede l’indicazione del tasso rapportato al capitale residuo e questo tasso risulta applicato in regime semplice.
Concludiamo che la rata, il cui importo è effettivamente conforme alla condizione del pagamento degli interessi di periodo sul capitale residuo, deve essere correttamente imputata, per le rispettive quote, ad interessi ed a capitale secondo la medesima condizione[24], purché nel contratto sia presente una corrispondente pattuizione (su come debba essere formulata, infra, par. 9 e 10). Se secondo il contratto sono legittimamente esigibili gli interessi maturati sull’intero capitale residuo non vediamo che significato possa avere ipotizzare che il creditore esiga invece interessi anatocistici su singole frazioni di capitale.
Il calcolo della rata secondo una formula in interesse composto ed il calcolo della quota interessi in regime semplice sono dunque compatibili dal punto di vista matematico, per la semplice ragione che fanno riferimento a due diverse basi di calcolo.
Rimane il fatto che il piano di ammortamento alla francese e quello costruito sulla base dei pagamenti attualizzati in regime composto prevedono, a parità di tasso di interesse, capitale mutuato, numero e frequenza delle rate, i medesimi flussi finanziari, e perciò sono ugualmente onerosi per il mutuatario; in altre parole, è dimostrato che il finanziamento alla francese è ugualmente oneroso, a parità di altre condizioni, di un finanziamento che prevede interessi anatocistici sul medesimo capitale.
E’ necessario domandarsi quali siano il significato finanziario e la rilevanza di questa identità. Per rispondere a questa domanda occorre in primo luogo considerare l’incidenza del tempo del pagamento degli interessi sul costo del finanziamento.
6. Il tasso effettivo.
La disciplina codicistica del contratto di mutuo non menziona il prezzo o costo del finanziamento, che solo in modo molto approssimativo si può dire sia rappresentato dall’interesse. Infatti il costo del finanziamento è determinato, oltre che dal valore del tasso, da altri elementi, in particolare gli oneri e le spese, che sono al di fuori del nostro tema di indagine e che considereremo pari a zero, ed il tempo del pagamento degli interessi, sul quale invece dobbiamo concentrare la nostra attenzione.
E’ un principio di base della teoria economica, ed un dato di comune percezione, che il medesimo importo monetario ha un valore diverso secondo che sia disponibile immediatamente o in un termine più o meno lungo; allo stesso modo il pagamento immediato è più oneroso, a parità di importo, del pagamento differito. Il costo del finanziamento così dipende anche dal tempo del pagamento degli interessi: finanziamenti del medesimo importo, della medesima durata, del medesimo tasso, con medesima scadenza del rimborso del capitale, e che prevedono il pagamento del medesimo importo di interessi[25] possono avere un costo diverso.
Ad esempio un finanziamento di 1000 € della durata di quattro anni con rimborso del capitale in unica soluzione alla scadenza finale, al tasso del 10%, e pagamento degli interessi al termine del finanziamento, in regime semplice, ed un finanziamento della medesima durata, importo, tasso, ma con pagamento degli interessi con cadenza annuale, comportano il pagamento di interessi del medesimo importo, pari a 400 €, ma il primo è, intuitivamente, meno oneroso del secondo.
Come è noto una misura oggettiva del costo del finanziamento è stata introdotta nel nostro ordinamento dalla legge n. 142 del 1992 con l’art. 19 primo comma: “E’ denominato tasso annuo effettivo globale (TAEG) il costo totale del credito per il consumatore espresso in percentuale annua del credito concesso e comprensivo degli interessi e degli oneri da sostenere per utilizzarlo, calcolato conformemente alla formula matematica che figura nell’allegato II alla direttiva del Consiglio 90/88/CEE.” La direttiva precisa che si tratta del tasso che rende uguali, su base annua, i valori attualizzati di tutti gli impegni pattuiti dal creditore e dal consumatore.
Nell’ammortamento alla francese certamente il pagamento degli interessi sul capitale residuo alla scadenza di ogni rata è una delle condizioni che ne determina il costo: il finanziamento sarebbe meno oneroso se gli interessi fossero esigibili solo alla scadenza finale o se fossero esigibili con ogni rata soltanto quelli maturati sulla quota di capitale in pagamento.
Un’altra condizione incidente sul costo, relativa al tempo di pagamento degli interessi, è la periodicità infrannuale: questa comporta un aggravio di costo rispetto alla scadenza annuale, perché determina una effettiva anticipazione del pagamento. Ma ipotizziamo per ora che la scadenza sia annuale, per due ragioni: perché la periodicità infrannuale non rientra fra le condizioni che definiscono l’ammortamento alla francese; perché è opportuno isolare gli effetti riferibili a cause differenti.
E’ naturale domandarsi quale incidenza abbia sul costo del finanziamento nell’ammortamento alla francese il pagamento degli interessi “anticipati”, ipotizzando che la scadenza della rata sia annuale e che non vi siano altri oneri; oppure in altre parole quale sia la maggiorazione del tasso effettivo[26] rispetto al tasso nominale indotta dalla “anticipazione” del pagamento degli interessi rispetto all’esigibilità del capitale.
La risposta, assolutamente banale per quanti si sono accostati alla materia con consapevolezza degli aspetti matematici[27]: la “anticipazione” del pagamento degli interessi non determina alcuna maggiorazione del tasso effettivo che è uguale al tasso nominale. Due corollari: il tasso effettivo in caso di differimento del pagamento di tutti gli interessi al termine del finanziamento è inferiore al tasso nominale; nell’ammortamento alla francese la maggiorazione del TAEG rispetto al TAN deriva solo dai costi, dalle spese, e dalla periodicità infrannuale.
Questa risposta potrebbe suscitare sorpresa, perché la maggiorazione del costo del finanziamento al contrario è di frequente data per evidente e presentata come un argomento di peso nella valutazione della legittimità dell’ammortamento alla francese ma, è il caso di ribadirlo, è del tutto pacifica.
E’ necessaria una spiegazione, che diamo in termini intuitivi e pratici.
Supponiamo di avere la disponibilità di un capitale di 1.000 € e di poterlo impiegare (prestare) al tasso di mercato del 10% annuo per la durata di un anno, ricevendo in restituzione al termine dell’anno la somma di 1100 €. Si tratta di un finanziamento monoperiodale, nel quale non si pone neanche l’alternativa fra interesse semplice e interesse composto, che presenta evidentemente un tasso effettivo pari al tasso nominale.
Supponiamo ora invece di avere l’opportunità di impiegare la medesima somma per la durata di due anni, ricevendo al termine del secondo anno 1200 €, pari al capitale maggiorato degli interessi semplici maturati in due anni al tasso del 10%.
Probabilmente ci renderemo conto che questa seconda alternativa è meno conveniente, perché se prestiamo la somma ad un anno possiamo riscuotere al termine dell’anno 1100 € e reimpiegarli nuovamente al tasso del 10%, in modo da ritrovarci al termine del secondo anno con 1210 €, con 10 € in più.
Se vogliamo ottenere lo stesso tasso effettivo del 10% stipulando un unico finanziamento abbiamo, astraendo da vincoli legali, due alternative: prevedere il pagamento annuale degli interessi, in modo da riscuotere 100 € alla scadenza del primo anno, che potremmo reimpiegare al medesimo tasso ottenendo alla scadenza del secondo anno i 10 € di differenza; oppure pattuire l’interesse composto, in modo da riscuotere dopo due anni 100 € di interessi maturati nel primo anno ed altri 110 € maturati nel secondo anno.
Il pagamento periodico degli interessi quindi assicura il mantenimento del tasso effettivo al livello del tasso nominale.
Invece il mero differimento del pagamento al termine finale determina una discesa del valore del tasso effettivo rispetto a quello del tasso nominale, in misura crescente con la durata del finanziamento, con la conseguenza che per mantenere un tasso effettivo dato occorrerebbe pattuire un tasso contrattuale sempre crescente, sino a raggiungere valori spropositati[28].
Abbiamo così individuato una ulteriore buona ragione a sostegno del pagamento “anticipato” degli interessi, che integra le considerazioni svolte nel par. 4: solo questa modalità rende confrontabili finanziamenti di diversa durata – due finanziamenti di diversa durata, medesima frequenza dei pagamenti e medesimo tasso hanno il medesimo costo effettivo – e da sempre, cioè da prima che esistessero calcolatrici finanziarie, programmi di calcolo, indici legali di costo, è in grado di fornire a chiunque, anche sprovvisto di qualsiasi cognizione matematica, una misura attendibile del costo del finanziamento.
L’identità fra il costo effettivo in caso di pagamento anticipato e di applicazione di interessi composti è recepita nella formula matematica utilizzata per il calcolo del tasso effettivo, che è basata sul regime composto.
L’equazione che lega il capitale, le rate, il tasso di interesse effettivo, è la seguente
C = R1/(1+i) + R2/(1+i)2 + … + Rn/(1+i)n
dove C è l’importo del capitale mutuato e R1, R2, … Rn, sono gli importi dei pagamenti rateali; si può riconoscere la presenza del fattore di sconto in regime composto, il che vuol dire che il capitale è pari alla somma dei valori delle rate attualizzati al momento iniziale in regime composto.
La formula restituisce un tasso di interesse che realizza la condizione di eguaglianza in regime composto; abbiamo già rilevato che questo tasso coincide, nell’ipotesi di periodicità annuale, con il tasso contrattuale.
A questa caratteristica della formula si riferiscono le critiche di chi le imputa la sua incapacità di evidenziare la maggiorazione di costo indotta dal pagamento periodico degli interessi[29].
Ma l’uso del regime composto per la valutazione delle operazioni di durata pluriennale, da sempre prescritto dalla normativa europea e nazionale, conformemente alla prassi internazionalmente adottata in matematica finanziaria, ha un saldo fondamento sia normativo sia tecnico; in particolare vi è un generale consenso sul fatto che, se pure è astrattamente possibile indicare un TAEG o un TAE in regime semplice, solo in regime composto sono confrontabili prestiti di durata diversa, mentre il TAEG in capitalizzazione semplice è dipendente dalla durata del finanziamento[30].
L’importo della rata è legato al capitale ed al tasso di interesse dalla medesima relazione che esprime l’eguaglianza dei valori futuri al valore attuale. E’ intuitivo che la formula per il calcolo della rata si ricava sostituendo a R1, R2, … Rn la rata costante x
C = x/(1+i) + x/(1+i)2 + … + x/(1+i)n
e risolvendo l’equazione assumendo come incognita tale valore.
Possiamo ora iniziare a rispondere alla domanda formulata alla fine del paragrafo precedente.
Il calcolo della rata secondo una formula in interesse composto riflette l’identità di costo effettivo, a parità di altre condizioni, fra un prestito che preveda il pagamento di interessi “anticipati” ed un prestito che preveda il pagamento di interessi differiti composti: se il costo effettivo è il medesimo è intuitivo che a parità di capitale erogato, tasso contrattuale, durata del finanziamento, numero e frequenza dei pagamenti, l’importo della rata costante debba essere il medesimo.
Trova così logica spiegazione l’utilizzo per il calcolo della rata di una formula in interesse composto, mentre rimane il problema, se a questa equivalenza di costo possa attribuirsi un significato giuridico, che sarà esaminato nel successivo par. 8.
7. Un normale prestito a rimborso progressivo.
Questa identità di costo effettivo dipende esclusivamente dalla “anticipazione” del pagamento degli interessi.
Infatti per tutti i finanziamenti a rimborso progressivo, in qualunque modo sia determinata la rata, compresi quelli che prevedono il pagamento periodico dei soli interessi ed il rimborso del capitale alla scadenza (comunemente detti oggi bullet), la relazione che lega il capitale ai pagamenti ed al tasso di interesse effettivo è la stessa che abbiamo riportato sopra:
C = R1/(1+i) + R2/(1+i)2 + … + Rn/(1+i)n
Questo vuol dire che qualunque prestito a rimborso progressivo, anche il prestito con ammortamento all’italiana, nel quale le quote di capitale sono costanti e la rata è decrescente, anche il bullet, può essere decomposto in una pluralità di prestiti elementari del tipo zero coupon che, se sommati, ricompongono il prestito originario[31] e, specularmente, che la singola rata di ciascuno di questi prestiti può essere espressa come il montante in interesse composto di una frazione del capitale mutuato, che sommata alle altre restituisce l’intero capitale originario.
Questo enunciato, anch’esso assolutamente pacifico in matematica finanziaria, può apparire controintuitivo, soprattutto nella sua applicazione al bullet, ma in realtà è comprensibile se si considera che nell’equazione sopra riportata i pagamenti dovuti figurano esclusivamente per il loro importo. In altre parole ciò che rileva è soltanto quanto è stato corrisposto dal mutuante e quanto, ed in che tempi, sarà restituito dal mutuatario. Restano al di fuori della formula sia il tasso indicato nel contratto (i è il tasso effettivo) sia la composizione dei pagamenti del debitore in capitale ed interessi, poiché essa prende in considerazione solo i flussi finanziari ed è indifferente al modo in cui questi sono stati contrattualmente determinati. E’ naturale del resto che solo da questi dipenda il costo effettivo e che finanziamenti diversi dal punto di vista contrattuale ma che determinino i medesimi flussi finanziari debbano avere il medesimo costo effettivo.
Quindi in un finanziamento del tipo bullet R1, R2,…, Rn-1 saranno gli interessi pagati periodicamente, Rn comprenderà anche la restituzione del capitale, e questi valori saranno tutti considerati come il montante di una quota di capitale determinata dal loro importo attualizzato in regime composto alla data di erogazione del prestito, esattamente come abbiamo visto nella ricomposizione della rata dell’ammortamento alla francese.
Ad esempio ipotizziamo un prestito di 1000 € per tre anni con pagamento annuale degli interessi, al tasso nominale del 10%, che preveda il pagamento di 100 € euro alla fine del primo e del secondo anno ed al termine del terzo anno il pagamento di altri 100 € di interessi e la restituzione del capitale, e così la restituzione di 100 € dopo un anno, di altri 100 € dopo due anni e di 1100 € dopo tre anni.
Questo prestito viene decomposto in tre ZCB: il primo della durata di un anno, necessariamente in interesse semplice, di 90,90 € con restituzione dopo un anno del capitale e degli interessi del 10%, per un totale di 100 €; il secondo, della durata di due anni, di 82,60 € con restituzione al termine del capitale e degli interessi composti al 10%, per un totale di 100 €, il terzo, di 826,50 €, della durata di tre anni, con restituzione al termine del capitale e degli interessi composti al 10%, per un totale di 1100 €. Si vede facilmente che la somma degli importi originari dei prestiti elementari restituisce il capitale del prestito unitario (90,90+82,60+826,50=1000).
Come per l’ammortamento alla francese, l’identità di tasso effettivo si traduce nella possibilità di esprimere il medesimo prestito in interesse composto.
La matematica finanziaria ci espone dunque queste due conclusioni, che dovrebbero apparire sorprendenti rispetto allo stato della questione in giurisprudenza:
- la specifica composizione della rata dell’ammortamento alla francese non ha alcuna incidenza né sul presunto anatocismo né sulla maggiorazione di costo, che dipenderebbero semmai unicamente dall’anticipazione del pagamento degli interessi;
- l’ammortamento alla francese sotto questo aspetto pone esattamente gli stessi problemi dell’ammortamento all’italiana e del bullet.
E’ irrilevante in sostanza non solo la specifica composizione della rata propria dell’ammortamento alla francese ma anche il fatto stesso che vi sia o non vi sia la restituzione graduale del capitale. La ragione è quella colta dalla giurisprudenza citata nel par. 3: essendo la quota capitale delle rate in scadenza costantemente detratta dal capitale, sul quale gli interessi sono calcolati, la sua restituzione è neutra rispetto all’onerosità del finanziamento, che rimane la medesima, espressa dal tasso effettivo; il costo effettivo è determinato, a parità di tasso nominale, dalla legge che regola il pagamento degli interessi, la quale è indipendente dalle quote di rimborso del capitale, e quella comunemente adottata, per tutti i finanziamenti a rimborso progressivo, è il pagamento periodico degli interessi maturati sul capitale residuo.
Se il tasso effettivo è identico, è diverso però l’importo complessivo degli interessi, maggiore nel bullet e nel prestito alla francese e minore nell’ammortamento all’italiana. La ragione è che nel bullet il mutuatario ha la disponibilità dell’intero capitale, che restituisce solo alla scadenza finale, per tutta la durata del finanziamento, e nell’ammortamento alla francese lo restituisce più lentamente rispetto all’ammortamento all’italiana, godendo complessivamente nel corso del finanziamento di un credito maggiore.
Alla luce di questi rilievi l’affermazione corrente secondo la quale l’ammortamento alla francese sarebbe più oneroso rispetto dell’ammortamento all’italiana perché “privilegia” la restituzione degli interessi rispetto alla restituzione del capitale[32] si rivela il frutto di un equivoco: il modo corretto di valutare l’onerosità di un finanziamento è guardare al tasso effettivo; dire che l’ammortamento alla francese è più oneroso dell’ammortamento all’italiana è un po’ come dire che è più oneroso, alle medesime condizioni, prendere a prestito 15.000 € invece di 10.000 €[33].
Per analoghe ragioni non si condivide la tesi, che è stata avanzata in dottrina, secondo la quale il problema dell’ammortamento alla francese attiene all’imputazione della rata costante, cioè alla distribuzione degli interessi nelle rate con un importo inizialmente maggiore e poi decrescente[34]. Essa presuppone implicitamente la pattuizione dell’importo della rata come autonoma ed indipendente da quella relativa al pagamento degli interessi, e dotata per sé stessa di una intrinseca forza restitutoria, ed ipotizza che l’intermediario realizzi, a danno del mutuatario, uno “scambio” fra restituzione del capitale e pagamento degli interessi. In senso contrario osserviamo che le parti possono stabilire liberamente i termini della restituzione rateale del prestito, e tale pattuizione è logicamente indipendente da quella che regola il pagamento degli interessi; stabilita quest’ultima e stabiliti il numero e la frequenza dei pagamenti, l’importo della rata e la sua composizione sono obbligate[35].
Questo è particolarmente evidente nella prima rata, nella quale la quota interessi, qualunque sia la forma di ammortamento prescelta, è identica, essendo pari al prodotto fra il tasso di interesse ed il capitale mutuato, ed è identica a quella del bullet; ma anche nelle rate successive opera la medesima regola, variando unicamente, per effetto della graduale restituzione del capitale, la base di calcolo.
Supponiamo ad esempio che il cliente in fase di conclusione del contratto, resosi conto che la prima rata è costituita al 90% da interessi, chieda di imputare il medesimo importo in conto capitale. La banca ben potrebbe rispondergli che per mantenere il medesimo equilibrio dello scambio tale maggiore importo della quota capitale dovrebbe aggiungersi agli interessi, comunque calcolati sul capitale iniziale, e non sostituirli, e proporgli un diverso piano di ammortamento, di minore durata, con rata pressoché doppia, una restituzione più rapida e quindi un minore importo di interessi, ma a parità di tasso effettivo.
Essendo unica, per tutta la durata del finanziamento, la legge che regola il pagamento degli interessi, il peso relativo della quota interessi all’interno della rata, che varia nel corso della sua durata, ha un valore del tutto estrinseco e non si può attribuire alcuna specifica rilevanza al fatto che essa sia in una prima fase maggiore della quota capitale; in particolare questo fatto non può essere considerato come indice del pagamento di interessi non maturati[36], perché il meccanismo di calcolo degli interessi è sempre il medesimo ed assume come base di calcolo il capitale residuo, mentre il rapporto fra la quota interessi e la quota capitale non ha sotto questo aspetto rilevanza alcuna.
L’assunto iniziale peraltro è il frutto di una generalizzazione infondata: mentre l’importo della quota interessi della prima rata è determinato in ogni caso dal prodotto fra il tasso di interesse ed il capitale iniziale, l’importo della quota capitale è condizionato dalla durata del finanziamento e per questo sono ben possibili ammortamenti alla francese nei quali, pur crescendo con la progressione delle rate, è sin dall’inizio superiore alla quota interessi. Ad esempio un mutuo alla francese di 100.000 €, da restituirsi in 5 anni in rate annuali, al tasso del 10% annuo, prevede necessariamente rate di 26.379,75 €, la prima delle quali comprende 16.379,75 € di capitale ed il minore importo di 10.000,00 € di interessi; se invece ipotizziamo una durata di 10 anni, le rate diventano di 16.274,54 €, la prima delle quali comprende solo 6274,54 € di capitale e sempre 10.000,00 € di interessi[37] (questi due finanziamenti, come sappiamo, presentano il medesimo tasso effettivo, pari al 10%, ed ovviamente il pagamento di interessi in misura diversa, dipendente esclusivamente dalla loro diversa durata).
E’ parimenti infondata la conclusione che si trae da questa affermazione, che in caso di estinzione anticipata del finanziamento o di decadenza dal beneficio del termine, gli interessi corrisposti sino a quel momento, o una parte di essi, debbano considerarsi privi di causa giustificativa perché non ancora maturati[38].
In realtà alla scadenza di ogni rata il mutuatario si trova ad avere pagato tutti gli interessi maturati sino a quel momento, e solo quelli, ed in più ad avere restituito una parte del capitale, pari alla somma delle quote capitale delle rate già pagate, e quindi ad avere un debito residuo pari alla somma delle quote capitale delle rate successive; potrebbe dunque estinguere il debito pagando istantaneamente questo importo, o rifinanziarlo. In questa seconda ipotesi, supponendo che il tasso di mercato sia rimasto invariato e che voglia mantenere ferma la durata e la periodicità del prestito, potrà ottenere da un altro istituto di credito le medesime condizioni, e continuare a pagare il medesimo importo delle rate; in caso di discesa del tasso di interesse, invece, potrà liberamente ricercare sul mercato le condizioni migliori; nessuna delle due cose gli sarebbe possibile se avesse pagato interessi non ancora maturati[39]. Si intende che il mutuatario nell’ammortamento alla francese in caso di estinzione anticipata potrà trovarsi di fronte ad un debito residuo maggiore, rispetto ad altre forme di finanziamento, ma ciò dipenderà unicamente dal fatto che in precedenza avrà pagato di meno[40].
Per queste ragioni si deve anche escludere che il rapporto fra quota interessi e quota capitale, considerato, al di là della sua variabilità nella progressione delle rate, come elemento caratterizzante il singolo finanziamento, possa rappresentare un indice della sua maggiore o minore gravosità e dell’intensità degli effetti pregiudizievoli per il mutuatario imputati all’ammortamento alla francese[41].
In generale, se è vero che vi è interdipendenza fra il pagamento degli interessi e la composizione della rata precedente, questa interdipendenza opera in modo del tutto elementare, come in qualunque prestito a rimborso graduale, nel senso che la restituzione parziale del capitale diminuisce la base di calcolo degli interessi, con la sola particolarità, propria dell’ammortamento alla francese, che le quote di restituzione del capitale sono determinate in misura tale che sommate alle quote interessi danno il valore della rata costante.
Infatti il rimborso progressivo del capitale proprio dell’ammortamento alla francese determina ad ogni rata la diminuzione degli interessi; poiché la rata deve essere costante la quota capitale deve aumentare del medesimo importo di cui gli interessi sono diminuiti dalla rata precedente; il vincolo della rata costante impone di inserire in ogni rata una maggiorazione della quota capitale pari alla variazione negativa della quota interessi rispetto alla rata precedente, variazione che è sempre crescente secondo una progressione geometrica pari a (1+i), perché è pari ogni volta al prodotto fra il tasso di interesse e la quota capitale pagata nella rata precedente [42]. Questa progressione geometrica delle quote capitale si arresta col pagamento dell’ultima rata, che determina la restituzione integrale del finanziamento; nel medesimo arco di tempo vengono pagati gli interessi sul capitale via via decrescente, necessariamente decrescenti, che sommati alle quote capitali compongono la rata costante.
Analizzando in dettaglio l’importo totale restituito dal mutuatario possiamo osservare quanto segue:
- la somma di tutte le quote capitale, benché segua una progressione geometrica, è pari “per costruzione” all’importo totale del capitale mutuato, perché la quota capitale della prima rata è fissata ad un valore tale che nel momento in cui la progressione si arresta si verifica la restituzione integrale, il che esclude la presenza di criticità (si tratta della mera restituzione dell’importo nominale del capitale erogato);
- l’importo totale degli interessi corrisponde a quello del bullet, detratti ad ogni scadenza quelli la cui maturazione è preclusa dalla progressiva restituzione del capitale.
La famigerata formula dunque individua l’importo della rata costante che soddisfa simultaneamente le condizioni di partenza, ma la successione delle quote di restituzione del capitale che realizza non ha nulla di diverso, dal punto di vista del meccanismo di calcolo degli interessi e dell’onerosità – misurata correttamente dal tasso effettivo – da tutte le altre ipotizzabili, che non devono necessariamente essere riconducibili ad una regola predeterminata, potendo le singole quote essere determinate anche in modo del tutto arbitrario, dando vita ad ammortamenti soggetti al medesimo regime finanziario, se la legge che regola il pagamento degli interessi è la medesima[43].
Infatti si possono ipotizzare prestiti nei quali la restituzione del capitale è ancora più rallentata rispetto all’ammortamento alla francese, e che determinano la maturazione di un monte interessi maggiore, in una scala continua che vede al suo limite superiore il rimborso a scadenza, nel quale il capitale viene restituito solo al termine finale; ed è interessante notare che il bullet, pur non suscitando la medesima diffidenza, presenta le medesime presunte criticità imputate all’ammortamento alla francese, portate all’estremo: gli interessi sono pagati anticipatamente e calcolati sul capitale residuo, che coincide per tutta la sua durata con quello iniziale; la rata è esclusivamente imputata al pagamento degli interessi; i pagamenti eseguiti non hanno alcun effetto solutorio sul capitale, che rimane immutato sino alla scadenza; il mutuatario che voglia interrompere anticipatamente il rapporto deve restituire, o rifinanziare, l’intero capitale.
A conferma dell’irrilevanza della restituzione rateale del capitale e della composizione della rata si può anche osservare come in matematica finanziaria sia nota l’equivalenza fra il prestito alla francese ed una pluralità di prestiti bullet aventi per oggetto le singole quote capitale e termine alla scadenza di ogni singola rata, con pagamento periodico degli interessi semplici[44] (si intende qui che l’importo della quota capitale è quello, crescente nel tempo, proprio dell’ammortamento alla francese).
Il grafico che segue rappresenta la scomposizione di un finanziamento alla francese di dieci rate in altrettanti prestiti del tipo bullet. I tempi riportati sull’asse verticale rappresentano sia la scadenza delle rate del prestito unitario sia la scadenza finale di ciascuno dei presiti elementari.
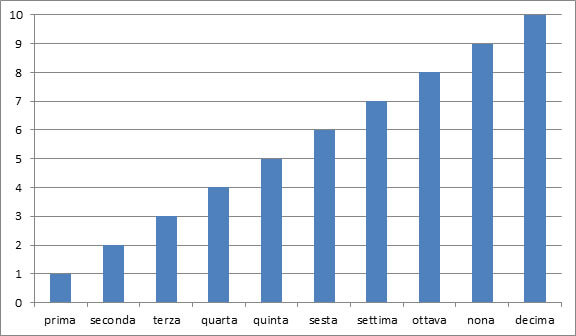
Come si vede ciascuno dei finanziamenti elementari, rappresentati dalle colonne (la cui altezza indica la durata e non l’importo), inizia al medesimo tempo 0. Il primo è un finanziamento monoperiodale che al momento 1 viene estinto col pagamento del capitale e degli interessi. Tutti quelli successivi pagano solo interessi ad ogni scadenza di periodo sino alla propria scadenza finale, quando restituiscono anche il capitale. Spostandoci sull’asse verticale, possiamo vedere che al momento 1 viene restituito il primo finanziamento (ricordiamo che corrisponde alla quota capitale della prima rata) e vengono pagati gli interessi di periodo relativi a tutti i finanziamenti elementari (ricordiamo che nella prima rata del prestito alla francese sono pagati gli interessi di periodo sull’intero capitale erogato); al momento 2 viene restituito il secondo finanziamento (corrispondente alla quota capitale della seconda rata) e vengono pagati gli interessi di periodo relativi a tutti i finanziamenti elementari escluso il primo, già estinto, e così via.
Naturalmente l’importo sul quale ai momenti 1, 2, …, 10 vengono corrisposti gli interessi corrisponde in ogni momento al capitale residuo del prestito unitario.
Questa scomposizione, diversamente da quella che abbiamo considerato al par. 5, lascia inalterata, rispetto al prestito unitario, la natura oltre che l’importo di tutti i movimenti, nel senso che gli importi del capitale e degli interessi pagati ad ogni momento sono i medesimi.
All’obiezione che i singoli prestiti elementari del tipo bullet sono a loro volta scomponibili in ZCB[45] si può quindi rispondere che quale sia la scomposizione espressiva della effettiva natura del finanziamento principale dipende in definitiva dalle pattuizioni negoziali e dai pertinenti principi giuridici[46], richiamando le considerazioni svolte nel precedente par. 5.
Pare evidente che se nessuno dei finanziamenti elementari presenta interessi composti si deve escludere che questi possano essere presenti nel finanziamento che risulta dalla loro somma. Pare ugualmente evidente che gli interessi sono computati esclusivamente sul capitale e che non vi è alcuna commistione di interessi e di capitale.
Concludiamo che le questioni sollevate nei confronti dell’ammortamento alla francese possono essere poste con riferimento a qualunque prestito che segua la medesima legge di pagamento degli interessi, e devono essere affrontate e risolte nel medesimo modo.
8. Regime composto ed interesse composto.
Infatti fra i critici, in ambito matematico-finanziario, prevale la tesi, basata sull’identificazione fra regime composto ed interessi composti, secondo la quale l’anatocismo è presente in tutti i prestiti caratterizzati dall’anticipazione del pagamento degli interessi[47], che ci sembra in effetti la più coerente.
In questa prospettiva si sostiene che il fenomeno dell’anatocismo è indissolubilmente legato al regime di interessi utilizzato, piuttosto che al tipo di ammortamento, e che l’unico modo per evitarlo è progettare il piano di ammortamento in regime semplice[48].
Il caposaldo di questa tesi è che come regola generale l’applicazione degli interessi richieda la preventiva scelta del regime finanziario e che l’opzione del diritto, espressa dagli artt. 1283 e 821 c.c., sia per il regime semplice; muovendo dall’assunto che nella prassi corrente gli interessi sarebbero applicati in regime composto essa propone, in considerazione dell’assenza e comunque dell’illegittimità della pattuizione di detto regime, di sostituirlo col regime semplice.
Essa si muove così sul piano dell’espressione della volontà negoziale, potendo il medesimo prestito, definito dai flussi finanziari, essere espresso in regime semplice o in regime composto.
Siamo di fronte all’alternativa fra due diversi linguaggi:
- secondo il linguaggio della “capitalizzazione composta” – ma noi diremmo secondo il linguaggio del diritto – un prestito di 1000 € al tasso del 10% annuo per 4 anni, ma in effetti di qualunque altra durata superiore all’anno, con rimborso del capitale alla scadenza finale, può prevedere il pagamento di interessi annuali al 10%, pari a 100 € da corrispondere alla scadenza di ogni anno;
- secondo il linguaggio della “capitalizzazione semplice”, fermi l’importo del capitale, la durata del prestito di 4 anni, il rimborso a scadenza, la frequenza dei pagamenti, per prevedere il pagamento di interessi annuali pari a 100 € occorre pattuire un tasso di interesse dell’11,45%., poiché questo è il tasso che realizza, in regime semplice, la condizione di equità finanziaria[49].
L’anatocismo così viene individuato non nell’applicazione e quantificazione degli interessi, ma in un momento successivo ed in un dato del tutto estrinseco, cioè nel fatto che la condizione di equivalenza finanziaria, per la quale il valore attuale di quello che si dà deve essere uguale a quello che si riceve, è realizzata in interesse composto, sostenendo che se questo si verifica siano necessariamente presenti interessi anatocistici.
Dal punto di vista operativo il linguaggio che si propone come quello corretto imporrebbe l’ausilio di un matematico anche per determinare quali siano gli interessi dovuti al 10% annuo, su un capitale di 1000 €, alla scadenza di ogni anno, cosa che altrimenti sarebbe delle più semplici; inoltre l’individuazione del tasso corrispondente ad un rendimento dato dipenderebbe dalla durata totale del finanziamento, e così se il finanziamento avesse una durata superiore, ad esempio di otto anni invece di quattro, per prevedere il pagamento di interessi annuali pari a 100 € occorrerebbe pattuire (v. par. 6) un tasso di interesse ancora superiore, anche se il rendimento effettivo sarebbe il medesimo.
Questa dipendenza del rendimento effettivo del finanziamento dalla sua durata appare difficile da giustificare sotto il profilo sia della razionalità economica sia della chiarezza del linguaggio.
Sul piano giuridico si deve osservare che la disciplina normativa degli interessi non contiene alcun riferimento al regime finanziario. Il diritto non detta una definizione dell’interesse ma la recepisce dalla tradizione giuridica e, sostanzialmente, dal linguaggio comune. Così, sotto il profilo strutturale, l’interesse è una prestazione commisurata in termini proporzionali ad una prestazione principale[50], ed il tasso non è altro che il rapporto numerico che esprime la relazione fra le due prestazioni, secondo il quale dall’importo dell’obbligazione principale si ricava l’importo dell’obbligazione accessoria; il tasso di interesse si identifica in questo rapporto e non nella parità finanziaria del prestito.
Così il rapporto fra i valori delle due prestazioni dipende dal tasso e dal fattore tempo ed è necessariamente lineare; questa linearità invece si perderebbe se davvero si dovesse ritenere che il tasso ed il tempo non siano sufficienti a determinare la prestazione dovuta, ma che debba aversi riguardo anche alla scadenza della prestazione principale. Ad esempio per un prestito di 1000 € che preveda il pagamento di interessi annuali del 10% sarebbero dovuti ogni anno per interessi, 100 € in caso di durata annuale, 954 € in caso di durata biennale, 914 € in caso di durata triennale, 878 in caso di durata quadriennale, 845 € in caso di durata quinquennale; pare evidente che il tasso di interesse non esprime più, da solo, la proporzionalità fra la prestazione principale e quella accessoria.
Il problema dell’anatocismo sorge solo nel momento in cui si ipotizza di aggregare al capitale gli interessi maturati nei periodi precedenti, in modo da maggiorare la base di calcolo, operazione che il diritto vieta o sottopone a condizioni particolari. L’identificazione del regime finanziario pertanto non è necessaria per l’applicazione del divieto di anatocismo.
Questa semplice conclusione ci sembra che trovi una conferma nel fatto che dovendo indicare un fondamento normativo all’opzione del diritto in favore del “regime finanziario semplice” non si è trovato di meglio che l’art. 821 c.c., che dispone al terzo comma che i frutti civili si acquistano, giorno per giorno, in ragione della durata del diritto. La disposizione, collocata nel terzo libro del codice, disciplina la ripartizione dei frutti civili in caso di successione nel diritto di godimento sulla cosa[51] e trova applicazione anche all’ipotesi che, per qualunque ragione, non sia possibile fare riferimento alla data di acquisto determinata dal titolo; essa sicuramente pone un criterio di proporzionalità al tempo, ma non vediamo cosa possa aggiungere alla proporzionalità intrinsecamente propria del tasso di interesse, né come da essa si possa trarre una regola sull’esigibilità degli interessi sui capitali, tanto meno nel senso del suo differimento al termine del prestito. Al contrario da essa si desume pianamente la regola dell’indifferenza del tempo del pagamento sulla quantificazione dei frutti civili, e quindi anche degli interessi (v. oltre, fine par. 9).
E’ importante ribadire che ciò che si assume determini il passaggio al regime composto è, semplicemente, l’anticipazione del pagamento degli interessi[52].
Questa assunzione necessariamente si riflette sulla costruzione del piano di ammortamento a rate costanti in “capitalizzazione semplice” che si propone in alternativa a quello proprio dell’ammortamento alla francese e nel quale infatti le quote interessi “risultano pari al prodotto tra il debito residuo relativo alla scadenza precedente, il tasso di interesse periodale e il fattore di attualizzazione per l’intervallo intercorrente tra la scadenza corrente e l’epoca finale dell’operazione di ammortamento.”[53](enfasi originale). E’ pacifico dunque che questo piano di ammortamento si fonda sull’attualizzazione dell’importo degli interessi, nonostante questi siano calcolati come prodotto tra tasso periodale e capitale residuo, in regime semplice, e dunque su una operazione di sconto diretta a compensare il mutuatario dell’onere della loro anticipazione: “La giustificazione economico-finanziaria della presenza dell’attualizzazione in CS [capitalizzazione semplice] è la conseguenza del fatto che gli interessi, maturati alla scadenza della rata, andrebbero pagati al termine dell’operazione di ammortamento, oppure, come considerato, in forma attualizzata, contestualmente alla scadenza della rata di riferimento.”[54] (nostra la sottolineatura).
Come si vede la riformulazione del piano di ammortamento in “capitalizzazione semplice” si fonda su due presupposti:
- l’assegnazione al tasso indicato nel contratto della funzione di esprimere, in regime semplice, l’equivalenza finanziaria del prestito, e sulla rideterminazione delle rate, con l’utilizzo del “fattore di attualizzazione” (altro elemento del tutto eccentrico rispetto alla disciplina normativa), in modo tale da ristabilire tale equivalenza, con conseguente decurtazione del monte interessi, in contrasto col criterio adottato sia dalla prassi sia dal diritto per la valutazione del costo delle operazioni finanziarie;
- l’assunto, prettamente giuridico, che il pagamento di interessi già maturati ma in anticipo sulla restituzione del capitale configuri anatocismo o comunque che il suo importo debba essere corretto in modo tale da rimettere il mutuatario in una situazione equivalente, dal punto di vista finanziario, al pagamento eseguito alla scadenza finale.
La questione di fondo è se, una volta stabilito che il pagamento anticipato degli interessi attrae il prestito nell’area del regime composto, questo dal punto di vista sostanziale equivalga all’applicazione di interessi anatocistici ed eventualmente se questa equivalenza possa assumere rilevanza ai fini dell’interpretazione dell’art. 1283 c.c., o comunque legittimare il concetto di “effetto anatocistico” o di “anatocismo sostanziale”.
L’equivalenza si ravvisa sotto il profilo del costo effettivo, che è identico, e sotto il profilo finanziario, nel senso che il pagamento anticipato degli interessi, come l’anatocismo, produce l’effetto di non lasciare sterili gli interessi maturati nel corso dell’operazione finanziaria, anche se in modo diverso, perché gli interessi pagati anticipatamente si trasformano in capitale in mano al creditore, mentre gli interessi anatocistici determinano un accrescimento del debito a carico del mutuatario. Questa relativa equivalenza peraltro non è una novità per il diritto, se nella relazione ministeriale al codice civile del 1865[55], in tema di anatocismo, a proposito degli interessi scaduti, si legge: “Se il debitore li pagasse, il creditore potrebbe impiegare la relativa somma ad interesse presso un terzo: perché si dovrà vietare che ciò si faccia lasciandoli a mani dello stesso debitore? Questi, inoltre, può non trovarsi in grado di pagare gli interessi dovuti senza ricorrere ad un prestito, sottoponendosi al pagamento di altri interessi; perché non dovrà ritenere quelli dovuti come nuovo prestito, invece di ricercare un terzo che abbia a mutuarglieli? Si teme che il debitore aumenti per tal modo eccessivamente il suo debito verso il creditore: ma la sua situazione non cambia punto, se aumenta il suo passivo obbligandosi verso un altro.”
La differenza rimane dal punto di vista effettuale, poiché i flussi finanziari sono differenti; nel medesimo esempio di un prestito quadriennale di 1000 € al tasso del 10% annuale: 100 € ad ogni scadenza annuale per tre anni e 1100 € alla scadenza del quarto anno, il pagamento anticipato; 1464 € alla scadenza del quarto anno, l’anatocismo.
Infatti per sostenere che l’anatocismo sussista anche nel primo caso si opera il ricalcolo del valore dei rimborsi all’epoca finale[56], in interesse composto – così evidentemente recependo l’interesse composto come il corretto parametro di confronto intertemporale – che dà il medesimo importo di 1464 €, ritenendo così dimostrata la presenza di interessi anatocistici pari a 64 €[57].
Ma siamo di fronte a due fattispecie oggettivamente diverse che non diventano identiche solo perché possiamo immaginare di sostituire nella prima i 100 € realmente restituiti annualmente per quattro anni con 464 € virtuali restituiti al termine dei quattro anni. La diversità di regime giuridico si fonda su questa oggettiva differenza: solo l’anatocismo determina la crescita del debito.
Il divieto si riferisce alle modalità di calcolo degli interessi, non alla loro entità, ben potendo le parti ottenere il medesimo rendimento effettivo dell’operazione in interesse semplice agendo sul tasso nominale; esso impedisce al debitore di assumere nel momento della conclusione del contratto, quando la sua accettazione potrebbe essergli richiesta come condizione necessaria per l’erogazione del credito, una obbligazione destinata potenzialmente ad una crescita indefinita, del cui effettivo onere potrebbe non rendersi conto[58], ed in questo senso è riconducibile ad una esigenza di trasparenza ante litteram.
Questa esigenza è palesemente del tutto insussistente di fronte al pagamento periodico degli interessi maturati, che è chiaramente espressivo della reale entità dell’impegno richiesto al debitore.
L’equivalenza fra pagamento anticipato degli interessi e anatocismo si rivela di fatto insussistente anche per altre ragioni, alle quali il giurista non dovrebbe essere indifferente[59]:
- il debitore pagando gli interessi periodicamente si libera del debito, mentre se li pagasse al termine dell’operazione sarebbe costretto o ad accantonarne l’importo, maggiorato degli interessi composti, o a reinvestirlo, assumendosene il rischio;
- se è vero che la riscossione anticipata degli interessi consente al creditore di metterli subito a frutto, e così di lucrare interessi da interessi, è vero anche che questi non sono a carico del debitore, perché provengono da altri investimenti estranei all’operazione di prestito ed il cui rischio è a carico del creditore.
Alla luce della ratio del divieto e della radicale diversità delle due fattispecie, non vediamo come sia ipotizzabile una sua estensione al pagamento anticipato degli interessi, né come si possano fondare valutazioni di indole sostanziale sull’identità del tasso effettivo[60]. La matematica finanziaria riconduce la capitalizzazione ed il pagamento al regime composto perché speculari: mentre l’interesse capitalizzato accresce la base di calcolo degli interessi a carico del debitore, l’interesse pagato anticipatamente è reso disponibile per un immediato nuovo impiego produttivo da parte del creditore, riducendo le somme a disposizione del debitore per impieghi fruttiferi. Il diritto invece si limita a precludere la formazione di nuovo debito mediante la maturazione di interessi sugli interessi già maturati. Il creditore di conseguenza può esigere gli interessi che maturano nel corso dell’ammortamento del mutuo prima della sua estinzione, non essendo obbligato a fare credito al mutuatario anche del loro importo ma potendo al contrario fare propria, dal momento in cui il mutuatario è obbligato a corrisponderli, la naturale fecondità del corrispondente importo monetario, che così gli è reso disponibile per altri impieghi[61]. Non siamo di fronte ad anatocismo ma ad un accordo che determina equivalenza finanziaria in regime composto.
La comune riconducibilità al regime composto sia degli interessi anatocistici sia del pagamento anticipato non può fondare dunque alcuna equiparazione in senso giuridico; il diritto non può automaticamente recepire l’utilizzo dei termini interesse composto e capitalizzazione composta comune in ambito finanziario e matematico. In questi ambiti “investire in interesse composto” significa porre in essere una operazione finanziaria che riconosce all’investitore il beneficio di liquidità relativo agli interessi maturati nel corso della sua esecuzione, “capitalizzazione degli interessi” può essere sinonimo del pagamento degli interessi maturati nel corso dell’ammortamento, “prestito in regime composto” è quello che determina l’equivalenza finanziaria fra quanto ricevuto e quanto restituito in interesse composto. Ma certo l’estensione del divieto di cui all’art. 1283 c.c. non può dipendere dal fatto che in matematica finanziaria si consideri o meno il regime composto come sinonimo di anatocismo, questione che ci pare meramente terminologica e che possiamo lasciare al confronto fra i matematici[62].
9. La forma di espressione negoziale delle condizioni contrattuali: il tasso di interesse.
Esaurito l’esame di quelli che abbiamo definito gli elementi strutturali dell’ammortamento alla francese, nel loro rapporto con gli aspetti di criticità imputati a tale figura, passiamo all’esame del modo in cui essi devono trovare espressione nella manifestazione della volontà negoziale, sotto i due distinti profili del requisito della determinatezza/determinabilità dell’oggetto del contratto e della disciplina di trasparenza contrattuale.
La distinzione fra i due profili è netta quanto alla ratio ed al punto di incidenza delle prescrizioni normative[63]: il primo esprime una elementare esigenza di individuazione del contenuto del contratto, che è soddisfatta se l’accordo, eventualmente integrato da regole legali, consente di stabilire gli elementi strutturali del rapporto e di determinare i diritti e gli obblighi delle parti; il secondo attiene ad una esigenza di maggior tutela dell’utente bancario in termini di chiara esposizione e di effettiva consapevolezza delle condizioni contrattuali, da attuarsi sia mediante condotte antecedenti o concomitanti alla conclusione del contratto sia mediante l’obbligatoria inserzione nel contratto di determinate indicazioni, indipendentemente dal fatto che queste siano necessarie per integrare il suo contenuto dispositivo.
Costituisce un aspetto della trasparenza anche l’esigenza di consentire al cliente di valutare, sulla base di informazioni precise e comprensibili, le conseguenze economiche potenzialmente significative delle sue scelte negoziali, cui si riferisce la sentenza della Corte di Giustizia del 3 marzo 2020, in causa C-125/18, Marc Gómez del Moral Guasch v. Bankia SA, relativa al rapporto fra previsione di un tasso variabile e disciplina consumeristica, citata nell’ordinanza del tribunale di Salerno. Tuttavia dobbiamo rilevare l’estraneità del profilo relativo all’incertezza sul futuro al nostro tema di indagine, essendo questo limitato al mutuo a tasso fisso, ed essendo di conseguenza la prestazione dovuta dal mutuatario esattamente determinata sin dal momento iniziale.
Nella prospettiva della trasparenza si deve ritenere che l’obbligatorietà dell’indicazione nel contratto del tasso di interesse, e di “ogni altro prezzo e condizione praticati” (art. 117 comma 4 Testo Unico Bancario) vada al di là della mera determinabilità della prestazione intesa secondo il parametro dell’art 1346 c.c., ed imponga l’esplicitazione del criterio convenzionale secondo il quale questa è determinata, non essendo soddisfatta dalla mera accettazione del suo risultato, trasfuso nella sua quantificazione.
In questo senso è plausibile che l’esatta individuazione della prestazione dovuta dal mutuatario, determinata dal numero e dall’ammontare delle rate, possa non essere sufficiente, se manca l’esplicitazione e l’accettazione del criterio secondo il quale il piano di ammortamento è stato costruito, e tanto più se è il risultato dell’applicazione di un tasso di interesse superiore a quello pattuito.
Infatti quando la prestazione sia stata determinata sulla base di una condizione non esplicitata, sostanzialmente secondo una scelta dell’intermediario fra più opzioni ugualmente possibili per il contratto, è evidente che l’accettazione da parte del cliente della quantificazione finale della prestazione, se pure può soddisfare il requisito della determinatezza dell’oggetto, è insufficiente sotto il profilo della trasparenza. Si dovrebbe porre invece un problema di indeterminatezza dell’oggetto quando vi sia incompatibilità fra una condizione espressa nel contratto e la quantificazione finale della prestazione operata nello stesso.
Secondo il Testo Unico Bancario, in caso di mancanza o inidoneità dell’indicazione del tasso di interesse, trova applicazione il tasso sostitutivo previsto dall’art. 117 comma 7, restando così esclusa radicalmente l’ipotesi della nullità totale del contratto.
Poiché abbiamo parlato di TAN, di TAEG, di tasso effettivo, è naturale domandarsi quale sia il tasso di interesse di cui è necessaria l’indicazione nel contratto.
Ricordiamo la definizione di interesse che abbiamo sopra riportato[64]; è questa che, essendo l’unica che abbia valenza generale, individua il tasso di cui si richiede l’indicazione nel contratto. Invece l’indicazione di parametri di costo imporrebbe la preventiva definizione di tali parametri e, ai fini della determinatezza del contratto, la specificazione del modo in cui da questi parametri si debba ricavare matematicamente il tasso di interesse che esprime il rapporto fra la prestazione principale e la prestazione accessoria. Infatti gli indicatori di costo devono essere inseriti nei contratti solo quando siano normativamente previsti e non in sostituzione ma in aggiunta al tasso di interesse propriamente inteso.
A questo proposito si possono richiamare le recenti decisioni della corte di cassazione che, confermando il prevalente orientamento della giurisprudenza di merito, hanno qualificato il TAEG come un mero indicatore sintetico del costo complessivo dell’operazione di finanziamento, non rientrante fra i tassi, prezzi ed altre condizioni la cui mancata indicazione in forma scritta è sanzionata dall’art. 117 del Testo Unico Bancario (Cass. Sez. 1, sentenza n. 39169 del 09/12/2021; Cass. Sez. 1, ordinanza n. 4597 del 14/02/2023).
Si comprenderà dunque che il tasso di interesse che deve essere obbligatoriamente inserito nel contratto coincide con quello che sinora abbiamo indicato come TAN, la prima aggettivazione dell’acronimo riferendosi semplicemente all’unità temporale di riferimento e la seconda costituendo un’avvertenza della sua possibile non coincidenza con il costo effettivo del finanziamento.
Il fatto che il TAN possa non corrispondere – anzi di regola non corrisponda – al costo del finanziamento, non deve indurre a sottovalutarlo, poiché esso determina concretamente l’obbligazione restitutoria e realizza l’individuazione del contenuto della prestazione del mutuatario. Si tratta, in termini concreti, del tasso secondo il quale si deve verificare, dopo averlo rapportato alla periodicità della rata (v. oltre), la corretta quantificazione delle quote interessi del piano di ammortamento, nel loro rapporto con il capitale residuo.
E’ questo, per il diritto, l’unico tasso che, costituendo una condizione contrattuale, possa dirsi propriamente “applicato”, ed alla luce di quanto esposto nei paragrafi precedenti possiamo escludere che nel prestito alla francese sia ravvisabile l’applicazione di un tasso diverso.
Altro è il problema relativo al costo effettivo, che il legislatore ha risolto mediante l’obbligatoria indicazione del TAEG, e nel quale peraltro, come abbiamo osservato, operano fattori che non dipendono dalla struttura dell’ammortamento.
La periodicità infrannuale, in particolare, produce una maggiorazione del tasso effettivo, indipendente dalla specifica composizione della rata dell’ammortamento alla francese, conseguente all’anticipazione del pagamento degli interessi rispetto alla periodicità annuale nella quale è espresso il TAN. Questo perché il tasso periodale viene calcolato come una semplice frazione del tasso annuale – ad esempio il tasso mensile è fatto pari ad 1/12 del TAN – senza tenere conto dell’onere determinato dall’anticipazione del pagamento, determinando così un tasso annuo effettivo (TAE) superiore al TAN. Si tratta dell’effetto che nella logica della assimilazione dell’anticipazione del pagamento all’interesse composto viene definito come capitalizzazione infrannuale.
Si pone la questione se, quando il contratto prevede una periodicità infrannuale, il tasso di interesse sia correttamente espresso su base annuale, o se invece sia necessario indicare direttamente il tasso periodale, ad esempio mensile, o esprimere il tasso annuale in termini di TAE.
Al riguardo si deve osservare che una cosa è il tasso di interesse, altra la periodicità del pagamento degli interessi, che le parti possono determinare liberamente. Il tasso in quanto tale è un rapporto che non dipende dall’unità temporale utilizzata, come la velocità, che può essere espressa in base al secondo, al minuto o all’ora, restando la medesima. La convenzione corrente è di indicare il tasso di interesse riferito all’anno, senza che questo assuma il valore di una indicazione del costo effettivo, e l’individuazione del tasso periodale come mera riparametrazione del tasso annuale proporzionale alla durata del periodo appare sicuramente la soluzione più intuitiva.
Questa soluzione risulta corretta anche alla luce dell’art. 821 comma 3 c.c., che stabilisce che i frutti civili si acquistano giorno per giorno, in ragione della durata del diritto, e così afferma l’indifferenza del tempo del pagamento sulla quantificazione degli interessi.
Infatti la corte di cassazione, richiamando questa norma, in diverse occasioni ha affermato che ove occorra determinare, sulla base di un saggio di interesse stabilito in ragione di anno, l’importo degli interessi dovuto per un periodo inferiore, bisogna semplicemente dividere l’ammontare degli interessi annuali per il numero di giorni che compongono l’anno e moltiplicare il quoziente per il numero dei giorni da considerare, criterio che ovviamente è equivalente all’applicazione di un tasso riparametrato alla durata del periodo.
In particolare la questione era stata posta con riferimento all’art. 6 della legge 6 dicembre 1962 n. 1643, relativa alla nazionalizzazione delle imprese elettriche, che dopo avere disposto che gli indennizzi fossero corrisposti in dieci anni con un interesse annuale del 5,50% disponeva che il pagamento avvenisse in venti rate semestrali eguali, ed è stata risolta dalla corte di cassazione affermando che per ogni semestre fosse dovuta la metà degli interessi calcolati ad anno, cioè il 2,75%[65].
Concludiamo che il tasso di interesse è correttamente indicato come TAN, anche quando il contratto prevede rate di periodicità infrannuale.
Altra condizione attinente all’interesse, oltre al tasso, è la periodicità del pagamento; abbiamo visto che il pagamento degli interessi alla scadenza di ogni rata è una delle condizioni caratterizzanti l’ammortamento alla francese. Questa condizione è espressa normalmente nei contratti dalla previsione secondo cui con ciascuna rata sono corrisposti sia gli interessi sia una quota del capitale, che ci sembra assolutamente adeguata, poiché la previsione del pagamento rateale costituisce fissazione espressa del termine di pagamento[66]; la periodicità indicata nel contratto determina dunque l’esigibilità, alla scadenza di ogni rata, del pagamento degli interessi.
Infine, l’individuazione del capitale residuo come base di calcolo degli interessi discende ex lege dal loro carattere compensativo e dalla naturale onerosità del mutuo[67].
10. La forma di espressione negoziale delle condizioni contrattuali: il piano di ammortamento.
Possiamo da subito escludere che all’indicazione testuale della modalità di ammortamento “alla francese” possa attribuirsi un qualche rilievo ai fini della necessaria determinatezza del contratto o ai fini del rispetto della disciplina di trasparenza. Infatti, benché tale denominazione possa considerarsi riassuntiva di una serie di caratteri ben definiti, essa è priva di un significato codificato o universalmente accettato, e tanto meno chiaramente comprensibile al cliente medio. Se poi fosse da intendere nel generico significato di mutuo a rata costante sarebbe comunque superflua, giacché l’importo della rata è sempre indicato.
Il piano di ammortamento è definito dalle convenzioni sulla restituzione del capitale e sul pagamento degli interessi, che determinano l’importo della rata.
Quando una condizione del contratto è definita univocamente in applicazione di parametri riportati nel testo negoziale, o è legata alle altre da un rapporto di interdipendenza o di necessaria conseguenzialità tale che, fissate queste, anch’essa risulta univocamente individuata, un problema di determinatezza propriamente non si pone, poiché essa è determinabile senza alcun margine di incertezza o di discrezionalità, indipendentemente dalla difficoltà del calcolo necessario per pervenire al risultato finale e dalla perizia richiesta per la sua esecuzione (cfr. Cass. Sez. 3, sentenza n. 25205 del 27/11/2014 e Cass. Sez. 6-1, ordinanza n. 8028 del 30/03/2018).
Una relazione di questo tipo è espressa dalla formula che lega l’importo della rata costante al capitale, al tasso di interesse, al numero ed alla frequenza dei pagamenti, in modo tale che, determinati questi elementi, esiste un unico valore della rata che costituisce la soluzione dell’equazione. Sia l’importo della rata sia tutti questi elementi peraltro sono ordinariamente riportati nel contratto.
Nella prassi negoziale il piano di ammortamento è allegato ai contratti di credito ai consumatori relativi a beni immobili residenziali, ai quali si riferisce la direttiva 2014/17/UE del 4 febbraio 2014, ma non ai contratti di credito al consumo, che sono oggetto della direttiva 2008/48/CE del 23 aprile 2008, i quali generalmente si limitano ad indicare il numero, la frequenza e l’importo delle rate ed il fatto che esse sono comprensive di capitale ed interessi.
A proposito dei contratti di credito al consumo la Corte di Giustizia, nella sentenza Home Credit Slovakia a.s. v. Klára Bíróová del 9 novembre 2016 (C-42/15), ha affermato che l’art. 10, paragrafo 2, lettere h) e i), della direttiva 2008/48, deve essere interpretato nel senso che il contratto di credito a tempo determinato, che prevede l’ammortamento del capitale mediante versamenti consecutivi di rate, non deve precisare, sotto forma di tabella di ammortamento, quale parte di ogni rata sarà destinata al rimborso di tale capitale, e che al contrario queste disposizioni, in combinato disposto con l’articolo 22, paragrafo 1, della medesima direttiva, ostano a che uno Stato membro preveda un obbligo del genere nella sua normativa nazionale.
Invero, essendo anche la composizione delle rate vincolata dalle altre condizioni sopra menzionate, l’allegazione del piano di ammortamento recante, oltre all’indicazione del numero, della scadenza e dell’importo delle rate, anche quella della loro composizione in quota capitale e quota interessi, non è necessaria per la determinatezza del contratto.
L’allegazione del piano di ammortamento, nel senso sopra indicato, può dunque rilevare, secondo la specifica disciplina di riferimento, ai fini della trasparenza, ma non attiene alla determinatezza del contratto, come si desume anche da alcune pronunce della corte di cassazione[68].
Questo però non significa che quando il piano di ammortamento sia presente non debba essere valutato come parte del contratto.
A questo proposito è il caso di chiarire che l’accertamento della volontà delle parti non può essere vincolato dalla preventiva attribuzione a determinati documenti, comunque denominati, o a parti del medesimo documento, secondo criteri formalistici, come la loro denominazione o intestazione o la loro qualificazione come allegati, un valore inferiore, se essi sono richiamati e se la volontà delle e parti si è formata ed espressa su di essi allo stesso modo che su quello che invece si è deciso di assumere come il “contratto”. Va ricordata, a questo proposito, la qualificazione del piano di ammortamento da parte della giurisprudenza di legittimità come clausola contrattuale[69].
Si intende che il piano di ammortamento deve essere conforme alle condizioni previste nel testo negoziale, di cui deve costituire oggettiva applicazione – in questo senso è stato qualificato come “accordo esecutivo”[70] – e che l’eventuale difformità porrebbe un problema sul piano dell’interpretazione o della validità del contratto; tale qualificazione appare però talvolta piegata ad una peculiare opzione interpretativa: individuare nelle restanti pattuizioni contrattuali, in realtà nella formula matematica che si assume implicita nel calcolo della rata costante, l’interesse composto, per poi trascurare la chiara indicazione di segno contrario che emerge dall’importo delle quote capitale e delle quote interessi riportato nel piano di ammortamento, da cui si desume invece l’applicazione di interessi semplici sul capitale residuo.
La questione che viene sollevata sul piano di ammortamento, in relazione al requisito della determinatezza ed al rispetto della trasparenza, si riferisce alla sua costruzione secondo la formula in interesse composto ed alla mancata indicazione di questa nel contratto.
L’idea sottostante è che l’interesse possa essere applicato in regime semplice o in regime composto, e che questa alternativa ponga un problema distinto dall’anatocismo, di completezza o di trasparenza del contratto, perché pur non essendovi anatocismo, almeno non “in senso giuridico”, come talvolta si precisa, il regime composto comporta degli effetti sfavorevoli per il mutuatario, specificamente la maturazione di un maggior ammontare di interessi e l’applicazione di un tasso effettivo superiore a quello dichiarato.
In questo senso è esemplare una recente sentenza di merito[71].
Questa decisione per prima cosa, conformemente all’orientamento prevalente, ha rilevato che gli interessi sono calcolati unicamente sul capitale residuo e che ad ogni scadenza quelli maturati risultano interamente corrisposti, e per questa ragione ha escluso la presenza di interessi anatocistici “nel senso classico del termine”, e la violazione del divieto di cui all’art. 1283 c.c.
Sotto un diverso profilo, relativo alla censura di indeterminatezza del tasso contrattuale, ha ritenuto necessario verificare quale sia stata la formula matematica utilizzata per quantificare l’interesse e se questa sia stata esplicitata nel contratto.
Per questa ragione ha disposto la rinnovazione della consulenza tecnica “1) per stabilire se il regime di capitalizzazione applicato al piano di ammortamento sia stato semplice o composto e, in questo secondo caso, 2) per stabilire se la capitalizzazione composta fosse chiaramente individuabile in contratto e se il tasso nominale convenuto fosse chiaramente determinato. […]”.
Il consulente d’ufficio ha risposto che “non è il sistema di ammortamento c.d. “alla francese” che implica necessariamente l’applicazione di interessi anatocistici, bensì il regime finanziario sottostante”, ed ha proceduto alla rideterminazione del piano di ammortamento, sempre “alla francese” (si intende a rata costante) ma in regime di “capitalizzazione semplice”.
Risulta dai passaggi della CTU riportati nella decisione che il consulente ha individuato la capitalizzazione composta nella legge finanziaria posta alla base del calcolo delle rate e ne ha desunto che anche le quote interessi sono calcolate in regime composto, utilizzando il consueto argomento, di sicura efficacia retorica, secondo cui sarebbe paradossale sostenere il contrario.
La sentenza ha quindi individuato nella capitalizzazione composta una specifica forma di calcolo degli interessi, qualificata come una condizione economica del rapporto, che come tale doveva essere espressa nel contratto, idonea a determinare l’applicazione di un tasso superiore a quello pattuito, e di conseguenza ha fatto propria la riformulazione del piano di ammortamento prospettata nella CTU in “capitalizzazione semplice”, con ricalcolo delle quote interesse “in forma attualizzata”, ed applicazione del tasso sostitutivo ex art. 117 Testo Unico Bancario.
Rimane inespresso il passaggio logico secondo il quale la c.d. capitalizzazione composta individua una specifica forma di calcolo degli interessi distinta dall’anatocismo. Non si comprende quale sia questa specifica formula di calcolo degli interessi, ed in cosa differisca dall’unica che conosciamo, riferibile alla singola unità di tempo, tasso periodale per capitale, tanto più alla luce dell’iniziale individuazione, quale base di calcolo degli interessi, del capitale residuo.
L’assunto di fondo, pur se inespresso, rimane quello dichiarato nella nota sentenza del tribunale di Bari-sez. Rutigliano n. 113 del 29 ottobre 2008, est. Mastronardi: che debba esplicitarsi il tasso effettivo del mutuo secondo la legge dell’interesse semplice (Cfr., art 1284 c.c.), per la quale detto interesse è la differenza, alla fine del rapporto, fra l’importo rimborsato e quello prestato.” (nostra la sottolineatura). Questa stessa decisione peraltro esponeva in modo abbastanza chiaro che la presunta applicazione di un tasso superiore a quello effettivo è semplicemente la conseguenza dell’anticipazione del pagamento degli interessi: “se da un lato, il creditore può scegliere di imputare il rimborso prima agli interessi che al capitale o proporzionalmente ad entrambi o, ancora, al solo capitale: dall’altro lato, lo stesso creditore, nel momento in cui viene convenuto il tasso contrattuale, deve tenere conto dell’incidenza sui costi, che comporta la modalità prescelta per il rimborso, e sul tasso, che deve restare sempre pari a quello contrattualmente convenuto.”
In effetti l’operazione compiuta dal consulente, e recepita dal giudice, è quella descritta nel par. 8: l’assunzione del tasso indicato nel contratto come il tasso che deve realizzare, in regime semplice, la condizione di equivalenza finanziaria; l’attualizzazione delle quote interessi in modo da compensare il debitore dell’anticipazione, rispetto alla data di scadenza finale, del pagamento degli interessi; la conseguente rideterminazione dell’importo delle rate in modo da ristabilire l’equivalenza finanziaria in regime semplice. Così quando si chiede al consulente di verificare se sia stata applicata la capitalizzazione composta la risposta sarà necessariamente positiva, se gli interessi dono stati calcolati sul capitale residuo; abbiamo spiegato le ragioni per cui questo non comporta interessi anatocistici; la c.d. capitalizzazione composta in realtà nulla è di diverso dall’esigibilità alla scadenza di ogni rata degli interessi calcolati al tasso periodale sul capitale residuo.
Dovrebbe risultare chiaro che il maggior tasso che si assume applicato in luogo del TAN espresso nel contratto è – al netto della “correzione” degli effetti della divergenza fra TAN e TAE, sulla quale non ritorniamo – il tasso che esprime l’equivalenza finanziaria in regime semplice e che la presunta maggiorazione degli interessi riflette unicamente la mancata accettazione della regola del pagamento periodico degli interessi maturati.
In questo modo il tasso indicato nel contratto perde la sua funzione propria, determinativa degli interessi dovuti per il singolo periodo di tempo, ed assume quella di un indice di costo[72], al di fuori di qualsiasi comprensibile riferimento normativo, secondo un criterio, quello del regime semplice, contrastante con quello generalmente adottato, e recepito dal diritto, per la valutazione del costo delle operazioni finanziarie, e si recepisce in pieno, consapevolmente o meno, l’identificazione fra pagamento anticipato ed anatocismo.
Rinviamo, per l’esposizione delle ragioni per cui riteniamo questa operazione giuridicamente non corretta ed irrazionale, al precedente par. 8.
Ci limitiamo qui a ribadire che i suoi presupposti logico-giuridici dovrebbero valere rispetto a qualunque operazione finanziaria caratterizzata dall’anticipazione del pagamento degli interessi e che quindi si svolga in regime composto.
Consideriamo ad esempio un finanziamento bullet di 1000 €, durata decennale, TAN del 10%, periodicità annuale.
Questo finanziamento produce interessi di 100 € pagati annualmente per un totale di 1000 €, equivalenti in regime composto alla data finale a 1593,75 €, 159,37 € per anno; il suo TAN reale in regime semplice sarebbe dunque pari al 15,94% annuo invece del 10% previsto dal contratto; mentre il valore alla data finale dell’ammontare complessivo degli interessi pagati supererebbe di 593,75 € l’importo di 1000 € che sarebbe dovuto secondo il regime semplice.
Seguendo il medesimo criterio esplicitamente dichiarato nella sentenza barese del 2008 sarebbe necessario rideterminare il piano dei pagamenti in regime semplice; ipotizzando di tenere fermo il TAN contrattuale del 10%, ma di applicarlo “in capitalizzazione semplice”, dovrebbero essere dovuti annualmente, in luogo di 100 €, 71,80 €, cioè l’importo che realizza l’equivalenza finanziaria del prestito al tasso semplice del 10%; risulterebbe così che il contratto prevedeva il pagamento di interessi indebiti per un totale di 282 €.
E’ importante sottolineare che si tratta esattamente della medesima operazione recepita nelle decisioni che ravvisano nell’ammortamento alla francese l’applicazione occulta della capitalizzazione composta e di un TAN superiore a quello dichiarato.
Ragionando in termini di trasparenza contrattuale si dovrebbe presupporre che il cliente bancario il quale assume l’impegno di corrispondere annualmente interessi al 10% su un capitale di 1000 € si aspetti qualcosa di diverso dal dovere pagare 100 € per anno, o comunque che esista una regola, della cui ignoranza da parte sua la banca non dovrebbe approfittare, secondo la quale la pattuizione del tasso di interesse si dovrebbe intendere come rivolta a fissare il tasso che determina in regime semplice l’equivalenza finanziaria del prestito.
Questi presupposti sono però del tutto inconsistenti.
Alla luce di queste considerazioni escludiamo che si possa attribuire alla formula in interesse composto un ruolo autonomo nella determinazione dell’obbligazione restitutoria e che la c.d. capitalizzazione composta individui una specifica condizione determinativa del rapporto distinta dall’anatocismo: il regime composto degli interessi consiste o nell’aggiunta al capitale degli interessi maturati e nel conseguente incremento della base di calcolo degli interessi successivi o nel pagamento periodico degli interessi maturati; una terza alternativa non esiste e non viene nemmeno concretamente proposta. La formula, una volta escluso che possa determinare l’applicazione di interessi anatocistici o di fantomatici interessi in capitalizzazione composta, si deve considerare solo come una modalità tecnica per determinare l’importo che soddisfa simultaneamente tutte le condizioni previste dal contratto.
Del resto se la disciplina codicistica del mutuo individua l’obbligazione del mutuatario nella restituzione del capitale e nel pagamento degli interessi, dal punto di vista della determinatezza del contratto si richiede che siano determinati il tasso ed il tempo del pagamento degli interessi ed i tempi ed i modi della restituzione del capitale.
Così l’elemento che determina l’ammontare degli interessi esigibili ad ogni scadenza è l’importo totale del capitale restituito nelle rate precedenti, non la formula secondo la quale questo è stato determinato[73], e la successione delle quote di rimborso del capitale propria dell’ammortamento alla francese non è qualitativamente diversa da qualunque altra ipotizzabile.
Le parti ad esempio potrebbero determinare ciascuna quota di rimborso del capitale singolarmente, in funzione delle previsioni del mutuatario sull’andamento delle proprie disponibilità in corrispondenza delle diverse scadenze, con un monte interessi che potrebbe essere anche superiore rispetto all’ammortamento alla francese e non esisterebbe allora alcuna “formula” in grado di esprimere il criterio di calcolo, anche se il “regime” dell’operazione come sappiamo sarebbe il medesimo.
Sicché se il prestito alla francese indica, invece della formula, le quote di capitale di cui è dovuta la restituzione ad ogni scadenza, in perfetta aderenza all’art. 1819 c.c. che contempla la previsione contrattuale della restituzione rateale del capitale, in effetti realizza il massimo della trasparenza ipotizzabile; in caso contrario, in pratica quando il piano di ammortamento non è allegato al contratto, le quote di capitale da restituire nel corso dell’ammortamento sono oggettivamente determinate dalle condizioni contrattuali, ed il cliente è comunque informato, sin dalla conclusione del contratto, dell’importo che deve corrispondere ad ogni scadenza.
Peraltro dal punto di vista della comprensibilità da parte del cliente la formula matematica sarebbe sicuramente meno chiara sia della puntuale e specifica indicazione della consistenza e della distribuzione delle quote di rimborso del capitale contenuta nel piano di ammortamento sia del criterio che comunque normalmente si desume dalle pattuizioni contrattuali, la restituzione graduale del capitale in misura tale da determinare, sommato alla quota interessi, l’importo della rata costante.
A questo proposito osserviamo che l’informazione di trasparenza è finalizzata ad assicurare la comprensione del prodotto, una comprensione non fine a sé stessa ma diretta alla valutazione della sua convenienza ed alla sua comparazione con prodotti analoghi[74]; essa pertanto necessariamente deve riferirsi ad aspetti rilevanti in tale valutazione e suscettibili di incidere sulle scelte del cliente, ed è tanto più efficace quanto più è semplice, sintetica, conforme a nozioni di comune conoscenza e comprensione.
L’indicazione della formula di calcolo della rata si deve quindi considerare irrilevante così dal punto di vista della determinatezza del contratto come da quello della trasparenza.
Analogamente si deve considerare irrilevante l’indicazione del regime finanziario. Si tratta di una nozione estranea sia alla disciplina codicistica sia alle comuni conoscenze della clientela, e non necessaria per l’esplicitazione delle condizioni contrattuali, non essendo altro che l’espressione matematica dell’esigibilità ad ogni scadenza della totalità degli interessi maturati nel periodo di riferimento, che costituisce invece una condizione contrattuale di agevole comprensione ed intuitivamente conforme alla logica economica. Né è sostenibile che l’indicazione del regime finanziario possa essere imposta dalla necessità di rendere esplicito l’onere finanziario che consegue all’anticipazione del pagamento degli interessi; abbiamo visto infatti che questa anticipazione non determina per sé stessa alcuna maggiorazione del tasso effettivo ma, al contrario, è necessaria per mantenerlo al livello del tasso nominale.
In generale, l’accertamento di una carenza sotto il profilo della trasparenza presuppone che il cliente avesse una ragione, plausibile secondo un principio di buona fede e di ragionevolezza al quale anch’egli è soggetto, di ritenere che l’equilibrio di interessi si sarebbe situato ad un livello diverso; invece le condizioni che determinano l’onerosità del prestito sono normalmente tutte indicate nel contratto[75].
Infine, rileviamo che tutte le condizioni contrattuali, nella misura in cui concorrono a determinare l’importo della rata, concorrono alla determinazione del TAEG; per questa ragione nessuna delle contestazioni sollevate nei confronti dell’ammortamento alla francese, anche quando si ritenesse fondata, imporrebbe una correzione del suo valore[76].
11. Considerazioni finali.
Al termine di questo percorso fra le questioni controverse relative all’ammortamento alla francese certamente si deve confermare che si tratta di materia che presenta aspetti tecnici di elevata complessità; ne potrebbe derivare l’impressione che il giudice sia di fatto obbligato a rimettersi al giudizio di un consulente, col risultato che la decisione finirebbe col dipendere dall’adesione di questo all’una o all’altra scuola di pensiero o dalla dichiarata scientificità del suo giudizio.
Il pericolo è che conclusioni raggiunte in ambito matematico-finanziario, per finalità che certamente non sono né possono essere quella di decidere sulla validità dei mutui, vengano assunte quali indiscutibili regole di giudizio.
Ne abbiamo visto un esempio con la tesi secondo cui la definizione di anatocismo si dovrebbe desumere, sic et simpliciter, dalla matematica finanziaria, così che al giurista non sarebbe consentito rilevare che nella definizione proposta sono ricompresi fenomeni fattualmente diversi, il pagamento anticipato ed il pagamento differito con applicazione di interessi ulteriori sugli interessi maturati, e valutarli autonomamente in relazione alla fattispecie normativa.
Un altro pericolo è quello di recepire dalla matematica finanziaria concetti dei quali non si è approfondito il significato, e che dovrebbero essere maneggiati con molta attenzione. Così sembra quasi che stia diventando senso comune del giurista l’idea che esista un regime di calcolo degli interessi debitori, chiamato “capitalizzazione composta”, che sarebbe qualcosa di diverso dall’anatocismo e sarebbe compatibile col divieto di cui all’art. 1283 c.c., e che si debba porre il problema della sua necessaria previsione nel contratto; non ci sembra però che sia stato spiegato in cosa consista, in cosa si differenzi dall’anatocismo, perché non sia soggetto al divieto, ed in che modo possa essere ravvisato nella singola rata, cosa che dovrebbe costituire un problema almeno per chi riconosce che la quota interessi è pari semplicemente al prodotto fra tasso periodale e capitale residuo[77].
Come sempre, una buona parte della soluzione del problema è porre la domanda corretta.
Se viene sollevata una contestazione sull’entità della rata si dovrebbe partire dalla semplice considerazione che il debito del mutuatario è costituito esclusivamente dalla restituzione del capitale e dal pagamento degli interessi e che tutto quello che eccede l’importo del capitale deve essere imputato ad interessi; l’importo degli interessi dovuti dipende esclusivamente dalla base di calcolo e dal saggio di interesse e deve essere calcolato secondo il tasso previsto dal contratto e nel rispetto del divieto di cui all’art. 1283 c.c.
Muovendo da questi presupposti non mancherebbe la possibilità, soprattutto se il piano di ammortamento, completo della composizione delle singole rate, è allegato al contratto, di formulare, con l’ausilio di comuni nozioni di matematica (non finanziaria), contestazioni specifiche sull’anatocismo, su eventuali difformità dell’importo delle rate rispetto alle condizioni contrattuali, o sull’applicazione di condizioni non previste.
Le censure invece vengono sollevate solitamente in termini astratti, nei confronti del sistema di ammortamento in quanto tale, o nei confronti del “regime finanziario”.
Infatti l’ammortamento alla francese è già stato sottoposto al giudizio della corte di legittimità, che in diverse occasioni ha dichiarato i relativi motivi di ricorso inammissibili[78], e talvolta[79] ha rilevato la necessità di una verifica puntuale dell’importo delle rate e del criterio di calcolo degli interessi.
Sicuramente le soluzioni sarebbero radicalmente diverse se invece si dovesse dare per acclarato, come un dato scientificamente accertato, che il mutuo alla francese prevede la “capitalizzazione composta” e se sulla base di questo presupposto si reputasse necessario riformulare il piano di ammortamento in “capitalizzazione semplice”, secondo criteri la cui effettiva natura non ci sembra sinora adeguatamente compresa.
Qualche accenno ora alle implicazioni delle questioni trattate, e delle loro possibili soluzioni, sull’equilibrio economico dei contratti e sugli assetti di mercato.
Si afferma di frequente che il prestito alla francese sarebbe preferito dagli istituti di credito perché lo considerano più conveniente. Abbiamo visto che questo non è corretto rispetto ad altri tipi di prestito che prevedono modalità diverse di restituzione del capitale, come il prestito all’italiana ed il bullet, e che l’onerosità del prestito dipende solo dalla legge che regola il pagamento degli interessi. Aggiungiamo ora che se si dovesse affermare in via giurisprudenziale la tesi secondo cui la corretta forma di espressione degli interessi sarebbe quella che determina la parità finanziaria in regime semplice, questo, a regime, non inciderebbe sul tasso effettivo dei mutui, ma solo sulla formulazione dei contratti, inducendo gli istituti di credito ad individuare quel tasso nominale che consentirebbe loro di realizzare il rendimento atteso, corrispondente al tasso di interesse di mercato[80]. Né certo si può vedere alcuna ragione per cui il tasso effettivo dovrebbe mutare solo perché espresso in modo diverso, peraltro solo a livello di TAN, giacché il TAEG resterebbe immutato.
In realtà la ragione dell’ampia diffusione dell’ammortamento alla francese sembra quella più semplice, che per prestiti di importo elevato è preferibile la restituzione graduale, e che la restituzione in rate costanti, e non decrescenti come nell’ammortamento all’italiana, corrisponde normalmente all’interesse del mutuatario, il quale verosimilmente contrae il prestito nell’aspettativa che i propri redditi aumentino o rimangano costanti nel tempo.
Questo si dovrebbe tenere presente anche in una eventuale valutazione del prestito alla francese sotto il profilo della disciplina antitrust[81], unitamente al fatto che si tratta di un modello negoziale uniforme che non ha alcuna incidenza né sul livello del costo né sulla possibilità per i clienti di confrontare la convenienza delle diverse offerte.
Può essere utile infine riassumere le nostre conclusioni nel modo più sintetico:
- il nocciolo del problema dell’ammortamento alla francese è il tempo del pagamento degli interessi;
- le questioni sollevate sull’anatocismo, sul calcolo della rata, sulla sua ripartizione in quota capitale e quota interessi e sulla trasparenza sono riconducibili al tempo del pagamento degli interessi;
- la regola del pagamento degli interessi al termine di ogni singolo periodo di maturazione è assolutamente conforme al diritto;
- il regime composto che caratterizza l’ammortamento alla francese dipende esclusivamente dalla regola del pagamento degli interessi al termine del singolo periodo di maturazione, che è quella comunemente in uso in tutti i prestiti;
- non si giustifica per il diritto, né secondo la logica economica, l’applicazione agli interessi corrisposti al termine di ogni singolo periodo di uno “sconto” diretto a compensare il debitore dell’onere derivante dalla “anticipazione” del loro pagamento rispetto al termine finale dell’operazione;
- solo in questo consiste la c.d. riformulazione in “capitalizzazione semplice” del piano di ammortamento;
- la giurisprudenza che considera fondate le censure sollevate nei confronti dell’ammortamento alla francese ridetermina il piano di ammortamento in modo difforme rispetto alle condizioni contrattuali ed alle regole del diritto e secondo criteri che se fossero fondati dovrebbero essere applicati a tutti gli altri prestiti che seguono lo stesso regime.
In conclusione, è naturale domandarsi per quale ragione le critiche si rivolgano solo, o principalmente, nei confronti del prestito alla francese.
E’ stato osservato[82] al riguardo che il modo più semplice per costruire un ammortamento alla francese è quello di utilizzare una formula nella quale l’interesse composto è presente in modo evidente, mentre per l’ammortamento all’italiana ed il bullet, benché la relazione fra quanto si riceve e quanto si restituisce sia del medesimo tipo, si può procedere diversamente in modo molto intuitivo.
Aggiungiamo che solo per l’ammortamento alla francese poteva apparire astrattamente possibile che qualche criticità fosse presente nel meccanismo di determinazione e di composizione della rata, o nell’importo complessivo dei pagamenti, ma unicamente perché al pagamento degli interessi si sovrappone il pagamento delle quote di restituzione del capitale, di importo variabile, che può offuscare la visione del meccanismo di calcolo degli interessi, che in realtà non ha alcun carattere specifico e rimane del tutto banale. Non crediamo infatti che se si fossero prospettate, nei confronti di un prestito di 1000 € restituiti in unica soluzione dopo tot anni a fronte del pagamento di 100 € l’anno al tasso nominale del 10%, questioni relative all’anatocismo o all’imputazione dei pagamenti agli interessi piuttosto che al capitale o ancora alla loro anticipazione rispetto alla scadenza finale del prestito, queste avrebbero potuto aspirare nella giurisprudenza anche solo ad una esigua frazione della considerazione e del seguito che hanno ricevuto in questi anni le contestazioni rivolte all’ammortamento alla francese.
[1] L’ordinanza del tribunale di Salerno è stata commentata da ANNIBALI A. et al., L’ordinanza del Tribunale Civile di Salerno e la rimessione della Corte di Cassazione alle proprie Sezioni Unite, in attuariale.eu, CACCIAFESTA F., Un’ordinanza fondata su un equivoco (l’ammortamento francese secondo il tribunale di Salerno), in ILCASO.it, 23 ottobre 2023, MARCELLI F., Finanziamento con ammortamento alla francese. Le tematiche oggetto del rinvio pregiudiziale (ex art. 363-bis) alla Cassazione S.U. Prime considerazioni: la pattuizione distinta dall’adempimento, in assoctu, 21 dicembre 2023, MARZULLO L., L’ammortamento alla francese, vecchi problemi, nuove questioni: note su un dialogo tra diritto e matematica che continua ad essere difficile, in giustiziainsieme.it, 5 gennaio 2024, NATOLI R., I mutui con ammortamento alla francese, aspettando le Sezioni unite, in Dialoghi di Diritto dell’Economia, novembre 2023, SEMERARO M., Le Sezioni Unite sull’ammortamento alla francese: molti equivoci e un fondo di verità, in Dialoghi di Diritto dell’Economia, ottobre 2023.
[2] FERSINI P. e OLIVIERI G., Sull’“anatocismo” nell’ammortamento francese, in Banche e Banchieri, 2/2015, p. 134; CACCIAFESTA F., Sulla presunta indeterminatezza di alcuni contratti di prestito (e altro: a proposito di una sentenza del tribunale di Cremona), in ILCASO.it, 6 giugno 2023, p. 3: “quello detto “francese” (o “alla francese”) è un ammortamento caratterizzato dalla costanza della rata tra tutti quelli “progressivi”: categoria che prevede il pagamento periodico degl’interessi sul debito ancora non restituito alla data, accompagnato da una procedura di rimborso che può essere la più varia possibile. Risulta anche che questo è il significato che a quelle parole attribuiscono gli operatori. Designeremo d’ora in avanti questa tipologia di prestito con l’acronimo AFS (la terza lettera stando per “standard”)”, e poi oltre, p. 4: “ammortamenti a rata costante diversi dagli AFS non si riscontrano nella realtà”; v. anche MARCELLI R., Ammortamento alla francese: equivoci e pregiudizi. La sentenza del Tribunale di Roma, V. Carlomagno, n. 17766 del 19/09/19, in Ildirittodegliaffari.it, 15 ottobre 2019, p. 4: “Ancorché si riscontri un uso promiscuo del termine alla francese, a rigori, con tale ammortamento i padri storici della scienza finanziaria solevano individuare i piani nei quali ricorrono tre condizioni: i) rata costante; ii) ammortamento graduale, in regime finanziario composto; iii) interessi della rata calcolati sul debito residuo.” ed oltre, p. 5, nt. 6, dove l’A. esclude che uno dei principi regolanti la costruzione dei piani di ammortamento secondo la matematica finanziaria sia che, con il pagamento della rata, debbano essere riconosciuti tutti gli interessi maturati nel periodo cui la rata si riferisce, ma rileva che è questa la condizione impiegata dagli intermediari.
[3] Le citazioni della giurisprudenza di merito saranno limitate a precedenti ritenuti particolarmente significativi o esemplificativi delle questioni trattate; la sentenza più risalente a noi nota che esprime l’orientamento riferito nel testo è la sentenza del Tribunale di Benevento n. 1936 del 19 dicembre 2012, est. Genovese.
[4] Successivamente all’assegnazione alle sezioni unite, ma senza alcun confronto con la questione oggetto del rinvio, una ordinanza della sezione tributaria della corte di cassazione, n. 27823 del 2 ottobre 2023, si è così espressa: “Il metodo “alla francese’’ comporta […] che gli interessi vengano comunque calcolati unicamente sulla quota capitale via via decrescente e per il periodo corrispondente a quello di ciascuna rata e non anche sugli interessi pregressi. In altri termini, nel sistema progressivo ciascuna rata comporta la liquidazione ed il pagamento di tutti (ed unicamente de) gli interessi dovuti per il periodo cui la rata stessa si riferisce. Tale importo viene quindi integralmente pagato con la rata, laddove la residua quota di essa va ad estinguere il capitale. Ciò non comporta tuttavia capitalizzazione degli interessi, atteso che gli interessi conglobati nella rata successiva sono a loro volta calcolati unicamente sulla residua quota di capitale, ovverosia sul capitale originario detratto l’importo già pagato con la rata o le rate precedenti. In tale prospettiva, l’applicazione dell’interesse composto non provoca comunque alcun fenomeno anatocistico nel conteggio degli interessi contenuti in ogni singola rata (in tal senso, in tema di interessi convenzionali applicati ai contratti di mutuo e di leasing, v. Cass. n. 16221/2022; Cass. n. 9237/2020; Cass. n. 34677/2022).”
[5] Senza alcuna pretesa di completezza, in prevalenza fra i contributi più recenti e più facilmente reperibili: ARETUSI G. et al., Anatocismo ed usura nei mutui – profili civilistici: alla ricerca di un linguaggio comune tra Matematica e Diritto, documento finale del Convegno ASSUBA, Pistoia, 8 maggio 2020, in www.openstat.it; MARCELLI R., PASTORE A.G., VALENTE A., Ammortamento alla francese. Il regime composto e l’anatocismo: il genus finanziario e la species giuridica, in I Contratti, VI, 2019; MARCELLI R., Le criticità dell’ammortamento alla francese. Il ruolo nevralgico dei rimborsi del capitale, in assoctu.it, 5 settembre 2023; ANNIBALI A. et al., Considerazioni sull’onere implicito relativo al differenziale di regime finanziario nelle operazioni di prestito con rimborso rateale. Analisi e confronti tra metodologie di valutazione, in attuariale.eu; ANNIBALI A. et al., Anatocismo nei processi di ammortamento. Il rapporto scientifico dell’AMASES 2022/01. Considerazioni critiche di tipo matematico e giuridico, in attuariale.eu. E’ importante sottolineare che, diversamente da quello che potrebbe sembrare dalla motivazione di alcune sentenze di merito, anche fra i matematici si registrano posizioni diverse; citiamo qui solo il Rapporto Scientifico 2022/01 dell’Associazione per la Matematica Applicata alle Scienze Economiche e Sociali (Anatocismo nei piani di ammortamento standardizzati tradizionali), https://www.amases.org/rapporto-scientifico-2022-01 a cura di PRESACCO F. et al., rinviando, su punti specifici, alle citazioni contenute nelle ulteriori note.
[6] Sentenza del tribunale di Cremona del 12 gennaio 2022, est. Corini, p. 22: “la quota interessi è influenzata dalla quota capitale (poiché il capitale residuo ad ogni scadenza dipende dalla quota capitale che di tempo in tempo gli viene sottratta), che a propria volta dipende dall’importo della rata calcolato il regime composto.”; NARDONE D. e CAPPELLUTI F., Il regime finanziario di capitalizzazione composta degli interessi nei finanziamenti rateali: criticità e soluzioni, in IL CASO.it, 29 aprile 2020, p. 45: “gli interessi già maturati, scaduti e pagati, vanno a costituire quella parte delle rate non defalcata dal capitale residuo (−1) a seguito del pagamento della rata e quindi tali interessi, pur non andando a generare direttamente altri interessi (meccanismo anatocistico), comunque influenzano indirettamente la determinazione degli interessi nel periodo successivo (per effetto della minore riduzione del capitale residuo su cui questi ultimi sono calcolati) conseguendo, in termini di ammontare complessivo di interessi prodotti, l’identico effetto anatocistico.”; in senso contrario, CACCIAFESTA, Il “regime dei prestiti” osservazioni critiche su un articolo di D. Nardone e F. Cappelluti, in ILCASO.it 4 marzo 2023, p. 11, ID., Sulla presunta indeterminatezza di alcuni contratti di prestito cit., p. 21.
[7] Si deve precisare che qui viene in rilievo il tasso di interesse periodale, che coincide col TAN solo nell’ipotesi di pagamenti annuali, mentre nell’ipotesi di pagamenti infrannuali è pari ad una corrispondente frazione del TAN, ad esempio ad 1/12 in caso di pagamenti mensili; v. al riguardo il successivo par. 9.
[8] Sentenza del tribunale di Massa del 12 ottobre 2023, n. 2105/2018 R.G., est. Provenzano, che cita Annibali A., Barracchini C., Annibali A., Anatocismo e ammortamento di mutui “alla francese” in capitalizzazione semplice, 2016.
[9] Relazione al codice civile, 570.
[10] Cass. Sez. 3, sentenza n. 2593 del 20/02/2003: “A carico del mutuatario di somme di denaro sono poste due distinte obbligazioni. La prima è quella di restituire la somma ricevuta in prestito (art. 1813 c.c.). La seconda è quella di corrispondere gli interessi al mutuante, salvo diversa pattuizione (art. 1815. c.c.). Sono due obbligazioni distinte ontologicamente e rispondenti a finalità diverse.” La corte di cassazione, quando ritiene di dovere differenziare il regime dell’obbligazione di interessi rispetto a quello dell’obbligazione principale, è solita affermare che la accessorietà può riferirsi al solo momento genetico: Cass. Sez. 5, sentenza n. 2095 del 24/01/2023; Cass. Sez. 5, sentenza n. 24295 del 30/09/2019; Cass. Sez. 6-5, ordinanza n. 17020 del 25/07/2014; Cass. Sez. 5, sentenza n. 13080 del 15/06/2011; Cass. Sez. 2, sentenza n. 25047 del 27/11/2009; Cass. Sez. 1, sentenza n. 23746 del 16/11/2007; Cass. Sez. 5, sentenza n. 5954 del 14/03/2007; Cass. Sez. L, sentenza n. 9800 del 20/09/1991.
[11] BIANCA C.M., Diritto civile, IV, L’obbligazione, Milano, 1990, p. 175, per gli interessi convenzionali.
[12] SIMONETTO E., I contratti di credito, Padova, 1953, rist. 1994, p. 261; ASCARELLI T., Obbligazioni pecuniarie, in Comm. c.c. Scialoja-Branca, p. 589.
[13] MOSCO L., I frutti nel diritto positivo, Milano 1947, p. 71; MARINETTI G., Interessi (diritto civile), in Noviss. Dig. It., VIII, Torino, 1962, p. 862; LIBERTINI M., Interessi, in Enc. Diritto, XXII, Milano, 1972, p. 124, nt. 129 per gli interessi legali, mentre afferma la scadenza annuale degli interessi convenzionali; QUINTARELLI A., Leibniz e il mutuo feneratizio con ammortamento “alla francese” a rata fissa, in ILCASO.it, 30 aprile 2020, p. 7 ss.; NATOLI R., L’ammortamento “alla francese”: una questione di trasparenza, in Banca, borsa, titoli di credito, 2023, I, p. 207.
[14] DE LUCA N., Mutuo alla francese: anatocismo, indeterminatezza od altro. Di sicuro, c’è qualcosa che non va, in Banca, borsa titoli di credito, 2021, I, p. 245, secondo il quale riconoscere l’esigibilità degli interessi relativi ad un capitale non esigibile significa attribuire al creditore un corrispettivo per una concessione di liquidità di cui il mutuatario non avrebbe ancora goduto; v. anche ID., Interessi composti, preammortamento e costi occulti. Note sul mutuo alla francese e all’italiana, in Banca, borsa titoli di credito, 2019, I, p. 386 ss.; DOLMETTA, A margine dell’ammortamento «alla francese»: gravosità del meccanismo e sua difficile intelligenza, in Banca, borsa, titoli credito, n. 5/2022, p. 12 dell’estratto, secondo il quale l’esigibilità degli interessi alla medesima scadenza del capitale si desume dal fatto che essi maturano in ragione della durata del godimento del capitale.
[15] Cass. Sez. 3, sentenza n. 20904 del 27/10/2005; Cass. Sez. 1, sentenza n. 6022 del 16/04/2003; Cass. Sez. L, sentenza n. 6228 del 01/07/1994; Cass. Sez. 3, sentenza n. 2352 del 08/03/1988.
[16] BIANCA, L’obbligazione cit., p. 338 s.
[17] FERSINI-OLIVIERI, op. cit. p. 136 ss.; PRESACCO F. e ZIANI L., Sull’anatocismo nell’ammortamento progressivo: un’impostazione non convenzionale, in hal-02159365, p. 7; BARILLA’ G.B. e NARDINI F., Legittimità dell’ammortamento alla francese e lo “spettro” dell’anatocismo. Un po’ di chiarezza fra matematica e diritto, in Banca borsa titoli di credito, n. 5 2021, p. 687 ss.; CACCIAFESTA, In che senso l’ammortamento francese (e non solo esso) dia luogo ad anatocismo, in Politeia, 120/2015, il quale peraltro in Una proposta per superare il dialogo tra sordi in corso sull’ammortamento francese, con alcune osservazioni sul TAEG e sul TAN, in Riv. del Dir. Comm. e del Dir. Gen. delle Obbligaz., CXVII, 2019, p. 373 ss., propone una dimostrazione di come la rata possa essere determinata senza il ricorso ad una formula in interesse composto; su quest’ultimo punto v. anche QUINTARELLI A., Leibniz e il mutuo feneratizio cit., p. 15 e p. 21 ss.
[18] ARETUSI G., Costituzione del capitale e ammortamento: questioni relative al dibattito in atto in tema di anatocismo nei prestiti graduali, in www.openstat.it e ILCASO.it, 30 giugno 2022, p. 18: “l’argomentazione più spesso addotta per giustificare la presenza di anatocismo nei prestiti a rimborso graduale, è nel dire che la rata è calcolata in regime composto, mentre l’ammortamento è calcolato in regime semplice degli interessi: […] si tratta, anche in questo caso, di fake news, dal momento che il regime utilizzato per la costituzione del capitale si riversa direttamente nell’ammortamento. Affermare il contrario o insinuare dei dubbi a riguardo, ignorando i risultati scientifici dimostrati in matematica finanziaria, equivale a praticare un esercizio paralogistico, nell’inconsapevolezza dei risultati offerti dalla letteratura scientifica o, peggio ancora, sofistico nella consapevolezza di tali risultati.”; analogamente la sentenza del tribunale di Cremona già citata, p. 22: “la non coerenza di tale ragionamento è percepibile anche sulla base di un procedimento del pensiero di livello non particolarmente elaborato e senza una conoscenza approfondita della matematica finanziaria.”
[19] FERSINI-OLIVIERI, op cit., p. 151, indicano, fra le condizioni per il cui soddisfacimento è necessaria la adozione del regime finanziario della capitalizzazione composta, la seguente: “la quota interessi è data dal debito residuo alla fine del periodo precedente moltiplicato per il tasso di interesse periodale”; PRESACCO-ZIANI, op. cit., p 4 ss.; BARILLA’-NARDINI, op. cit., pag. 697 ss.; CACCIAFESTA, Un commento tecnico-matematico su una sentenza (Bari 1890/2020) in tema di ammortamento francese”, in Giurimetrica, 1/21: “la condizione “naturale” […] (che il debitore paghi periodicamente tutto l’interesse generato dal debito ancora non rimborsato) fornisce per la rata lo stesso valore che si ottiene con la formula in interesse composto.”
[20] Qualche semplice nozione di matematica finanziaria: secondo la formula dell’interesse semplice, gli interessi prodotti da un capitale C sulla base del tasso i sono pari a C per i per t, dove t rappresenta il tempo in anni e frazioni di anno; il fattore di capitalizzazione è definito come il rapporto fra il montante dell’operazione ed il capitale iniziale (il montante quindi è pari al prodotto fra il capitale iniziale ed il fattore di capitalizzazione); il fattore di capitalizzazione in regime composto è pari a (1+i)t ; la presenza del tempo (t) come esponente e non come fattore è tipica del regime composto; il fattore di sconto, o di attualizzazione, che determina il valore attuale di un capitale disponibile in futuro, è pari all’inverso del fattore di capitalizzazione e quindi in regime composto a v. CACCIAFESTA, Matematica finanziaria (classica e moderna), Torino 2006, p. 2 ss., ID, Le leggi finanziarie dell’interesse semplice e composto, e l’ammortamento dei prestiti, in assoctu.it.
[21] Il finanziamento con rimborso unico alla scadenza, senza pagamenti intermedi di interessi, è oggi usualmente denominato zero coupon bond (ZCB).
[22] Per esempi numerici di questa riformulazione del piano di ammortamento, v. MARCELLI, Ammortamento alla francese: equivoci e pregiudizi cit., p. 19 e QUINTARELLI, Leibniz e il mutuo feneratizio cit., p. 16.
[23] Secondo la sentenza del tribunale di Torino del 18 febbraio 2022, est. Astuni, l’applicazione di interessi composti su interessi maturati in periodi anteriori a quello della rata in pagamento, ma esigibili solo con questa, si dovrebbe ritenere sottratta al divieto normativo, che riguarderebbe, conformemente al tenore letterale dell’art. 1283 c.c., solo gli interessi scaduti, nel senso di esigibili; la tesi, più che sull’argomento letterale, si fonda sulla ratio del divieto, individuata nella tutela del debitore dal pericolo di una crescita indefinita degli interessi, sul rilievo che sotto questo profilo l’importo finale risultante dalla applicazione degli interessi composti, coincidente con l’importo della rata, è noto in partenza, e sulla natura delle eccezioni previste, la richiesta giudiziale e la convenzione posteriore alla scadenza, che sono riferibili esclusivamente ad interessi già esigibili. Ma come rilevato nella medesima sentenza l’estensione del divieto ad interessi non esigibili è stata riconosciuta da oltre un ventennio in materia di conti correnti; aggiungiamo che l’art. 1283 c.c. tutela un’esigenza di trasparenza in senso lato (v. par. 8), che non ci sembra sarebbe soddisfatta dall’indicazione dell’importo finale del debito; sotto questo aspetto non vediamo perché dovrebbe essere consentito all’autonomia negoziale di incrementare il debito, anteriormente alla sua esigibilità, applicando interessi composti invece di agire, in modo più trasparente, sul valore del tasso, tanto più in assenza della giustificazione normalmente invocata per l’anatocismo, l’esigenza di compensare il creditore della ritardata percezione degli interessi. Per queste ragioni riteniamo che la questione che viene sollevata sulla presenza nella rata di interessi anatocistici debba essere risolta invece alla luce delle considerazioni esposte oltre nel testo.
[24] QUINTARELLI, Ancora sul mutuo con ammortamento francese a rata costante e sull’anatocismo: le regole del diritto e della matematica finanziaria, in ILCASO.it, 17 settembre 2021, p. 17 nt. 31: “Che utilizzando diverse ripartizioni nella progressione delle quote capitale rispetto a quella ricavabile dalle convenzioni delle parti e dall’applicazione delle regole di legge si possano ottenere risultati diversi, oppure, attraverso algoritmi matematici strutturati in regime composto, risultati numericamente sovrapponibili, sono fatti che non rilevano sulla legittimità giuridica dell’operazione, che […] è conforme a quanto previsto e consentito dalle norme sul mutuo”; BARILLA’-NARDINI, op cit., p. 697: “sebbene la rata del mutuo venga determinata attraverso una formula finanziaria che prevede l’attualizzazione dei flussi finanziari mediante la formula dell’interesse composto, ciò non può certamente portare ad affermare l’esistenza di anatocismo, in quanto il calcolo degli interessi corrispettivi è sempre e comunque effettuato sul capitale residuo attraverso la formula dell’interesse semplice.”
[25] È importante distinguere fra il tasso di interesse, che è un numero espresso in forma percentuale, e gli interessi intesi come somma di denaro concretamente dovuta per la disponibilità di un capitale per una certa durata di tempo.
[26] Parliamo ora di tasso effettivo e non di TAEG perché l’aggettivo “globale” serve a includere gli altri oneri, che abbiamo supposto assenti, e perché l’aggettivo “annuale” è divenuto superfluo avendo supposto che la rata sia annuale.
[27] BARILLA’-NARDINI, op cit., p. 696; MANTOVI A. e TAGLIAVINI G., Anatocismo e capitalizzazione annuale degli interessi, in dirittobancario.it, giugno 2015, p. 7; CACCIAFESTA, Sulla presunta indeterminatezza cit., p. 4 e ss.; ID., L’ammortamento francese “in interesse composto”: un normale ammortamento progressivo, in ILCASO.it, 1° agosto 2021.
[28] MANTOVI-TAGLIAVINI, Anatocismo e capitalizzazione annuale cit., p. 3, e BARILLA’-NARDINI, op. cit., p. 695 s., i quali concludono: “Chi scrive non può credere che gli articoli 1283 e 821 c.c. prescrivano alle banche di formulare i contratti in questi termini.”
[29] COLANGELO G., Interesse semplice, interesse composto e ammortamento francese, in Foro Italiano, 2015, V, 469; ARETUSI et al., documento finale del Convegno ASSUBA cit., p. 39 ss.; ARETUSI, Trasparenza e opacità nella formula di calcolo del TAEG alla luce della sentenza Lexitor, in Rivista di Diritto del Risparmio, 3/23.
[30] BARILLA’-NARDINI, op. cit., p. 695; MANTOVI-TAGLIAVINI, Anatocismo e capitalizzazione annuale cit., p. 4: “L’uso della capitalizzazione annuale per operazioni di lunga durata è una convenzione di calcolo che ha numerosi vantaggi e che rende fattibili queste operazioni, altrimenti sostituite con operazioni a breve rinnovate nel tempo o sostituite con operazioni a tasso maggiorato.”; CACCIAFESTA, Le leggi finanziarie cit., p. 2 ss.
[31] FERSINI-OLIVIERI, op. cit., p. 141 ss.; CACCIAFESTA, Ammortamento francese e bullet: simul stabunt, simul cadent, note di commento al convegno Focus sul modello francese a rata costante del 4 dicembre 2020 organizzato da ASSOCTU ed ASSOTAG, in assoctu.it; ARETUSI, Brevi note sulla presunta assenza di anatocismo nei prestiti graduali in regime composto, con esempi per l’ammortamento francese, italiano e bullet, in ILCASO.it, 2 gennaio 2021; ID., Costituzione del capitale e ammortamento cit.
[32] V. ad esempio la sentenza del tribunale di Isernia del 28 luglio 2014, est. De Angelis, e la sentenza del tribunale di Roma n. 2188 dell’8 febbraio 2021, est. Basile; anche secondo la giurisprudenza dell’Arbitro Bancario e Finanziario l’ammortamento alla francese è “notoriamente più oneroso” dell’ammortamento all’italiana: così la decisione n. 14376 del Collegio di Coordinamento dell’8 novembre 2022 e le successive conformi decisioni dei collegi territoriali; in dottrina, DE LUCA, Interessi composti, preammortamento e costi occulti cit., p. 372.
[33] NATOLI, I mutui con ammortamento alla francese cit., p. 10: “Nell’ammortamento alla francese si pagano sempre, ceteris paribus (dunque a parità di tasso, durata e frequenza delle rate), più interessi rispetto all’ammortamento all’italiana perché il mutuatario gode più a lungo del capitale preso in prestito.”
[34] DOLMETTA, A margine dell’ammortamento «alla francese» cit., p. 15 ss. dell’estratto.
[35] Per le medesime ragioni risulta problematica la costruzione di un piano di ammortamento a rata costante e con quote costanti di capitale ed interesse. Non è possibile infatti determinare una quota di interessi costante, né se si assume come base di calcolo il capitale residuo, né considerando esigibili solo gli interessi maturati sulla quota capitale in pagamento: nella prima ipotesi la base di calcolo varierebbe ad ogni scadenza per effetto della restituzione graduale del capitale, determinando una quota interessi decrescente; nella seconda ipotesi la base di calcolo sarebbe costante, ma ad ogni scadenza sarebbero esigibili gli interessi maturati in un numero crescente di periodi, determinando un importo crescente della quota. V. al riguardo l’esempio proposto da DE LUCA, Mutuo alla francese cit., p. 243, ed i rilievi critici formulati da QUINTARELLI, Ancora sul mutuo con ammortamento francese cit., p. 18, nt. 36.
[36] Non si condivide, pertanto, quanto affermato, muovendo dall’assunto che l’ammortamento alla francese presenti necessariamente inizialmente una quota interessi superiore a quella capitale e successivamente la variazione e l’inversione del rapporto, in una ordinanza interlocutoria della corte di cassazione: “detto tipo di ammortamento comporta – per propria conformazione strutturale, seppur con intensità maggiore o minore a seconda delle fattispecie che nel concreto lo realizzino – che una parte degli interessi posti a remunerazione del mutuo erogato divengano esigibili prima che siano maturati, per maturare in epoca successiva alla scadenza fissata per relativo pagamento.” (Cass., sez. 6, ordinanza n. 14166 del 24/05/2021).
[37] Gli strumenti di calcolo sono disponibili sul portale della Banca d’Italia “L’Economia per tutti”.
[38] LIBERTINI, Interessi cit., p. 125, nt. 130, ammette la validità del patto di corresponsione di interessi non ancora maturati ma rileva che “nel caso in cui per una qualsiasi ragione il debito principale venga a scadenza in un momento antecedente a quello convenuto, saranno ripetibili gli interessi già pagati ma non ancora maturati”; ipotizza che questo possa verificarsi in caso di estinzione anticipata di un prestito alla francese DOLMETTA, A margine dell’ammortamento «alla francese» cit., p. 2 dell’estratto. Il problema si porrebbe allora, fra l’altro, con riferimento alla questione, oggetto della sentenza della Corte di Giustizia del 19 settembre 2019, C-383/18, c.d. “Lexitor”, e della sentenza della Corte Costituzionale n. 263 del 2022, sulla ripetizione dei costi del mutuo; v. al riguardo COLANGELO, “Lexitor” e Corte Costituzionale: esplode il contrasto fra il principio di proporzionalità e la formula esponenziale del Taeg, in Foro Italiano, 2023, c. 381, e ARETUSI, Trasparenza e opacità cit.
Nel senso del testo, invece, NATOLI, L’ammortamento “alla francese” cit., p. 214.
[39] In senso contrario FARINA V., Piano di ammortamento alla francese: liceità, meritevolezza e trasparenza della relativa clausola, in Rivista di Diritto Bancario, gennaio/marzo 2023, p. 162, “è pacifico che la banca, che percepisce anzitempo gli interessi su di un capitale il cui godimento altrui non è ancora scaduto, consegua una posizione di forza, idonea come è noto a precludere la portabilità del mutuo o a sconsigliare sotto il profilo della convenienza la pur legittima voglia di una estinzione anticipata, in ragione che nella maggior parte dei casi a residuare è solo buona parte del capitale, avendo già il debitore onorato gli interessi.”; nel senso del testo, NATOLI, ibidem.
[40] NATOLI, op. cit., p. 213: “la maggior somma necessaria per estinguere, alla medesima scadenza anticipata e nell’invarianza di tutti gli altri elementi, un mutuo alla francese rispetto a un mutuo all’italiana, è la naturale conseguenza del fatto che, pagando rate costanti, il cliente ha rimborsato meno capitale (di cui, dunque, ha goduto più a lungo) rispetto a quanto ne avrebbe rimborsato pagando rate decrescenti.”
[41] Secondo DOLMETTA, A margine dell’ammortamento «alla francese» cit., p. 18 dell’estratto, “tra l’applicazione di un ammortamento francese di tipo soft (quasi equilibrio tra l’imputazione a interessi e quella a capitale) e l’applicazione di un tipo hard (grande squilibrio di imputazione) può ovviamente correre una differenza enorme, sì che a un certo punto la quantità diventa per forza qualità (sul punto, le dinamiche nel concreto adottate per l’imputazione dei pagamenti, tra interessi e capitale, possono ben risultare illuminanti).”
[42] Se poniamo la quota capitale della rata n pari a Cn, la quota interessi della stessa rata è pari al tasso di interesse per il capitale residuo, che è dato dal capitale iniziale C meno le quote di capitale di tutte le rate precedenti
i (C – C1 – C2 – … – Cn-1)
la quota interessi della rata successiva Cn+1 è pari a i(C – C1 – C2 – … – Cn-1– Cn) quindi è diminuita del prodotto fra il tasso di interesse e Cn,, pari a iCn
poiché l’importo della rata deve restare costante la quota capitale deve crescere della medesima misura
Cn+1 = Cn + iCn = Cn(1+i)
quindi la quota capitale cresce ad ogni rata secondo una progressione di (1+i).
[43] V. CACCIAFESTA, In che senso l’ammortamento francese cit., p. 4.
[44] PRESACCO-ZIANI, op. cit., p. 16 ss.
[45] FERSINI-OLIVIERI, op. cit., p. 141 s.
[46] PRESACCO-ZIANI, op. cit., p. 35, rilevano l’apparente paradosso in forza del quale “un ammortamento progressivo tradizionale registrerebbe sia assenza (in corrispondenza di una scomposizione equivalente BB [bullet bond]) che presenza (in corrispondenza di una scomposizione equivalente ZCB) di interessi su interessi.”, per poi concludere: “la presenza o assenza di interessi su interessi non dipende a nostro avviso dal tipo di scomposizione, ma dalla premessa giuridica sulla cadenza di esigibilità degli interessi. A ben vedere il compito del matematico non è quello di sentenziare su questo punto ma solo quello di chiarire limpidamente gli sviluppi matematici coerenti con tali condizioni giuridiche.”
[47] In ambito matematico la tesi secondo cui il prestito alla francese presenta criticità specifiche, rispetto al prestito all’italiana ed al bullet, è sostenuta da MARCELLI, da ultimo in Le criticità dell’ammortamento alla francese cit. e in Finanziamento con ammortamento alla francese cit.
[48] ARETUSI, Brevi note cit., p. 7; ID, Costituzione del capitale ed ammortamento cit., p. 2.
[49] Per questo esempio v. ARETUSI et al., documento finale del Convegno ASSUBA cit., p. 24 ss.
[50] LIBERTINI, in Interessi cit., p. 95 rileva: “La nozione di «interesse» […] è abbastanza chiara, sia nel linguaggio comune che nella tradizione giuridica, sì che il legislatore, pur disciplinando in numerose norme l’obbligazione di interessi, non ha sentito il bisogno di precisarne la nozione, facendo affidamento sulla diffusione e sull’univocità della nozione tradizionale. Secondo quest’ultima «gli interessi sono quelle prestazioni accessorie, omogenee rispetto alla prestazione principale, che si aggiungono ad essa per effetto del decorso del tempo e che sono commisurate ad una aliquota della stessa»” (la definizione riportata dall’A. è di FERRARA F. jr., Il fallimento, 1966, p. 291).
[51] SGANGA C., Dei beni in generale, in Commentario al Codice Civile Schlesinger, 2015, p. 390.
[52]ANNIBALI et al., Anatocismo nei processi di ammortamento cit., p. 7: “l’esigibilità periodica degli interessi maturati in ciascun periodo è una caratteristica tipica ed esclusiva del regime finanziario della capitalizzazione composta, che quindi genera interessi su interessi precedentemente maturati.”
[53] ANNIBALI A. et al., Considerazioni sull’onere implicito relativo al differenziale di regime finanziario nelle operazioni di prestito con rimborso rateale. Analisi e confronti tra metodologie di valutazione, in attuariale.eu, p. 10.
[54] Ibidem.
[55] Citata da INZITARI B., Interessi. Legali, corrispettivi, moratori, usurari, anatocistici, Torino, 2017, p. 120.
[56] In matematica finanziaria per confrontare importi esigibili in epoche diverse è necessario riportare il loro valore ad un unico momento.
[57] Per questo esempio e per la relativa dimostrazione v. ARETUSI et al., documento finale del Convegno ASSUBA cit., p. 26 nt. 11.
[58] INZITARI, op. ult. cit., p. 124.
[59] Le evidenzia un matematico: CACCIAFESTA, Il “regime dei prestiti” cit., p. 6.; ID., Un’ordinanza fondata su un equivoco cit., p. 7 s. “Sappiamo bene che, da un certo punto di vista molto teorico, “pagare equivale a capitalizzare”. Sappiamo però anche bene che, dal punto di vista pratico (e non degli operatori professionali, ma dei normali fruitori del credito), pagare è l’opposto di capitalizzare: pagare vuol dire liberarsi (di una parte) del debito, capitalizzare vuol dire accrescerlo.”
[60] Cass. Sez. Trib. ordinanza n. 27823 del 2/10/2023, già citata, pur rilevando la genericità della deduzione, da parte del ricorrente, della realizzazione, mediante il sistema di ammortamento cd. “alla francese”, di un risultato anatocistico, aggiunge: “Ad ogni buon conto, è opportuno rilevare che l’art. 1283 c.c. vieta infatti la produzione di interessi su interessi scaduti ed è questa l’unica fattispecie ivi regolata.”
[61] QUINTARELLI, Ancora sul mutuo con ammortamento francese cit., p. 13 s. “La disponibilità degli interessi prima della fine del periodo di impiego del capitale è il fenomeno finanziario definito beneficio di liquidità, in quanto il creditore può immediatamente reinvestire quella somma per ottenere altri interessi. Senonché il beneficio di liquidità, se pur ricompreso, in ottica finanziaria, nel regime di capitalizzazione composta degli interessi, non integra la fattispecie dell’anatocismo. […] La matematica finanziaria non coglie questa rilevante distinzione ed eterogeneità giuridica tra i fenomeni diversi e distinti del “beneficio di liquidità” e dell’“anatocismo”: legittimo il primo (esigibilità/pagamento anticipato degli interessi rispetto al capitale che li genera), illegittimo il secondo (mancato pagamento degli interessi con produzione da parte di questi di altri interessi).”
[62] Sul punto v. le differenti posizioni di ARETUSI, Brevi note cit., p. 14 ss. e CACCIAFESTA, Il “regime dei prestiti” cit., p. 14, secondo il quale “Il termine stesso “anatocismo” non è, o non è più, conosciuto in Matematica Finanziaria”.
[63] SEMERARO, op. cit., p. 10.
[64] V. precedente nota 50.
[65] Dalla motivazione di Cass. Sez. U, sentenza n. 3797 del 23/11/1974: “La previsione della scadenza semestrale attiene alla cosiddetta «debenza» degli interessi, non alla «spettanza»; gli interessi vanno corrisposti cioè in scadenze semestrali, ma vanno pur sempre computati in percentuale annua. Il versamento semestrale non costituisce anticipazione, cui debba corrispondere uno «sconto», come è affermato nella sentenza impugnata. Al contrario gli interessi, che in linea di principio sono dovuti, come si è detto, giorno per giorno, vengono ad essere corrisposti a scadenza posticipata, al temine della maturazione semestrale. La disposizione che prevede l’eguaglianza dell’ammontare delle rate semestrali non induce a derogare all’applicazione della regola, giacché la parificazione ben può essere compiuta proporzionando opportunamente l’ammontare del capitale all’ammontare degli interessi in scadenza, senza che ciò richieda una diminuzione del debito di interessi.”; v. anche Cass. Sez. 1, sentenza n. 3224 del 25/10/1972, Cass. Sez. 1, sentenza n. 4647 del 10/08/1979 e Cass. Sez. 1, sentenza n. 191 del 27/01/1964, relativa ad altra fattispecie.
[66] Per questa ragione possiamo prescindere dalla soluzione della questione accennata nel par. 4, quale sia, in difetto di previsione negoziale, la regola di diritto suppletiva sull’esigibilità degli interessi.
[67] QUINTARELLI, Ancora sul mutuo con ammortamento francese cit., p. 7: “Gli interessi (compensativi) del mutuo si generano, naturalmente, dall’intero capitale mutuato e non da parti di esso, talché l’obbligo di pagamento degli interessi previsto dalle norme si riferisce anch’esso, pacificamente, a tutti quelli che maturano sul capitale trasferito al mutuatario per il tempo intercorrente dalla traditio alla sua restituzione per intero al mutuante”.
[68] Cass. Sez. 6 – 1, ordinanza n. 26426 del 08/11/2017: “In sede di opposizione allo stato passivo, la produzione del piano di ammortamento non costituisce elemento indefettibile della prova del residuo credito da mutuo, specie ove i requisiti costitutivi delle reciproche obbligazioni, ed in particolare quella restitutoria, risultino dalla chiara previsione contrattuale e dalla natura delle rate, dalla prevedibilità del loro importo per quota di interessi separata rispetto al capitale e si tratti di circostanze allegate al giudizio dal creditore, non bastando al riguardo una generica contestazione di rilevanza del curatore.”; v. anche Cass Sez. 3, ordinanza n. 12922 del 26/06/2020 (non massimata).
[69] Cass. Sez. 1, sentenza n. 33474 dell’11/11/21; Cass. Sez. 1, sentenza n. 23972 del 25/11/2010; Cass. Sez. 1, sentenza n. 5703 del 19/04/2002; Cass. Sez. 3, sentenza n. 2352 del 22/04/1981.
[70] CAMARDI C., Mutuo bancario con piano di ammortamento “alla francese”, nullità delle clausole sugli interessi e integrazione giudiziale, in Banca, borsa, titoli di credito, 2015, II, p. 54 s.
[71] Sentenza app. Bari n. 28 del 13.01.23, est. Binetti.
[72] Altra sentenza della corte di appello di Bari, n. 1890 del 3 novembre 2020, est. Romano, afferma, citando la consulenza tecnica d’ufficio: ”mentre in un regime di capitalizzazione semplice, il TAN può rappresentare una corretta misura del costo del finanziamento, esso ‘perde questa sua caratteristica in un regime di capitalizzazione composta (dal momento che la relazione tra tempo e interesse non è più lineare)’, ‘anzi in tali circostanze, per via della capitalizzazione, il TAN fornisce, come nel caso in esame, una misura sottodimensionata del prezzo costo dell’operazione…”.
[73] QUINTARELLI, Ancora sul mutuo con ammortamento francese cit., pag. 18, rileva che il monte interessi è “funzionalmente collegato, non tanto al regime finanziario di calcolo degli interessi, che dovendo svilupparsi per una sola frazione temporale tra rata e rata è indifferente che sia semplice (aritmetico) o composto (geometrico), quanto alla modulazione delle quote di restituzione del capitale nelle rate”.
[74] NIGRO A., in La legge sulla trasparenza delle operazioni e dei servizi bancari e finanziari: note introduttive, in Diritto della Banca e del Mercato Finanziario, 1992, p. 422, osserva: “l’informazione non rileva mai in sé: essa rileva sempre in funzione degli effetti che la conoscenza, come risultato del processo informativo, produce o è idonea a produrre. Tali effetti sono di tipo organizzativo, cioè di indirizzo, di conformazione dell’azione.”; MUCCIARONE G., in Ammortamento alla francese: meritevolezza e trasparenza, in Banca, borsa, titoli di credito, 2023, I, p. 604: “la trasparenza non è fine a sé; il mercato non deve capire ogni cosa del prodotto: a ciascuno la sua professione; l’informazione, per essere una buona informazione, dev’essere essenziale, ridotta a quel che strettamente serve al destinatario.”
[75] Si intende che l’esame è qui svolto in termini generali, con una ampia riserva rispetto alla astratta infinita variabilità dei casi individuali ed alla possibilità che il singolo piano di ammortamento sia difforme dalle condizioni contrattuali; inoltre ricordiamo che non stiamo considerando le spese, che devono essere obbligatoriamente indicate.
[76] Questo perché l’importo della rata, comunque sia stato calcolato, rientra direttamente nel calcolo del TAEG. Per la medesima ragione non avrebbe comunque fondamento l’inserimento nel tasso effettivo del presunto maggior costo determinato dall’applicazione del regime composto, ai fini della verifica del rispetto della soglia di usura, come invece ritenuto dalla sentenza del tribunale di Roma n. 2188 dell’8 febbraio 2021, est. Basile, e dalla sentenza del tribunale di Cremona n. 8 del 12 gennaio 2022, est. Corini, già citate; sul punto v. CACCIAFESTA, Anatocismo e usura (nota a sentenza del Tribunale di Roma 8 febbraio 2021), in eclegal.it, 30 marzo 2021, ID., Sulla presunta indeterminatezza di alcuni contratti di prestito cit., p. 19, MARCELLI, Le criticita’ dell’ammortamento alla francese vengono gradualmente emergendo. Sentenza del Tribunale Roma, F. Basile, n. 2188/2021, in assoctu.it, 15 marzo 2021.
[77] Naturalmente la risposta all’ultima domanda potrebbe essere che l’importo determinato in regime semplice alla data di scadenza della rata deve essere virtualmente convertito nel valore equivalente, in regime composto, alla data finale del finanziamento; ci pare evidente però che affermare semplicemente che si sia in presenza di una non meglio definita capitalizzazione composta degli interessi lasci in ombra questa conversione di valori, e soprattutto i suoi presupposti logico-giuridici, precludendo il necessario esame della loro fondatezza, che abbiamo condotto al par. 8.
[78] Cass. Sez. 1, ordinanza n. 13888 del 19/05/2023; Cass. Sez. 3, ordinanza n. 16221 del 19/05/2022; Cass. Sez. 1, sentenza n. 9405 del 12/04/2017; Cass. Sez. Trib. ordinanza n. 27823 del 2/10/2023, già citata.
[79] Cass. Sez. 1, ordinanza n. 34677 del 24/11/22 e Cass. Sez. 3, sentenza n. 9237 del 20/05/2020, rigettando il ricorso, hanno rilevato che in concreto il sistema di ammortamento effettivamente applicato non aveva dato luogo ad anatocismo, in quanto gli interessi venivano calcolati sul residuo e non sull’intero; Cass. Sez. 1, sentenza n. 33474 dell’11/11/2021, ha rilevato, quale motivo concorrente di inammissibilità del ricorso, che l’assunto del ricorrente, secondo cui le rate scadute incorporavano interessi non ancora maturati aveva carattere assiomatico, non specificando secondo quali parametri le parti avessero determinato l’ammontare delle singole rate e quale fosse l’importo delle quote capitale e delle quote interessi.
[80] CACCIAFESTA, Sulla presunta indeterminatezza di alcuni contratti di prestito cit., p. 5.
[81] Per uno spunto in questo senso v. DOLMETTA, A margine dell’ammortamento «alla francese» cit., p. 5 dell’estratto; v. anche NATOLI, I mutui con ammortamento alla francese cit., p. 5.
[82] CACCIAFESTA, Una proposta per superare il dialogo tra sordi cit., p. 13.


