SOMMARIO: Il lavoro spiega parametri e formule matematiche per l’elaborazione di un piano di ammortamento, cerca di risolvere i principali dubbi giuridici sulla validità dei contratti che prevedono ammortamenti alla francese, suggerisce clausole trasparenti al riguardo.
ABSTRACT: The paper explains parameters and mathematical formulas to develop a loan amortisation, tries to solve the main doubts about the legitimacy of the contracts which adopt a French amortisation, suggests clear contractual terms and conditions.
1. Introduzione e generalità
Questo breve scritto mira a eliminare i principali dubbi in ordine all’ammortamento di mutui, con particolare riguardo all’ammortamento con rata costante[1], indicando come descrivere in maniera trasparente le condizioni d’un ammortamento.
La presentazione è suddivisa in sezioni (e sottosezioni) per facilitare i riferimenti.
Anticipiamo un indice di massima.
- Introduzione e generalità
- Costruzione di un piano di ammortamento
2.1 Parametri rilevanti
2.2 Tassi d’interesse
2.3 Piano d’ammortamento
2.4 Preammortamento
2.5 Il caso di rate non costanti - Comuni contestazioni e loro infondatezza
3.1 Comuni contestazioni
3.2 Il regime composto implica anatocismo?
3.3 La mancata esplicitazione di calcolo implica indeterminatezza del contratto? Ammortamento e trasparenza
3.4 Differenziale d’interesse e soglia d’usura
3.5 Ammortamento, determinatezza e trasparenza
3.6 Ammortamento e imputazione dei pagamenti
Con un contratto di mutuo, il mutuante consegna al mutuatario una somma di danaro, che s’impegna a restituire a scadenza ovvero in più rate (art. 1813 del codice civile). Normalmente il mutuatario è obbligato anche alla corresponsione degli interessi (art. 1815, comma 2, del codice civile). Gli interessi maturano sul capitale non ancora restituito (art. 821 del codice civile).
Nel caso d’un contratto, di durata biennale, con scadenze semestrali delle rate: 1/2, 1, 3/2, 2, se le rate d’ammortamento sono d’ammontare superiore agli interessi dovuti (quota d’interessi), il loro ammontare decresce nel tempo: la differenza tra la rata e gli interessi dovuti (quota di capitale), nel caso di rata costante, cresce[2].
2. Costruzione di un piano di ammortamento
Nella pratica finanziaria[3] si può costruire un mutuo in due modi, partendo dalle quote di capitale oppure partendo dalle rate (inclusive d’interessi e capitale). I due modi sono equivalenti: la cosa è matematicamente provata[4]. Per mutui all’italiana è più naturale partire dalle quote di capitale, visto che esse sono costanti, mentre per mutui alla francese è più semplice partire dalle rate, visto che sono esse ad essere costanti.
Illustriamo la costruzione d’un ammortamento usando un semplicissimo esempio: è sufficiente per comprendere la meccanica. Esempi più complessi richiedono solo una massa di calcoli maggiore, ma la logica è la stessa.
2.1 Parametri rilevanti
Mostriamo quali siano i parametri rilevanti con riferimento al semplice esempio
| Ammontare del finanziamento | 1000 |
| Durata del finanziamento (anni) | 2 |
| Cadenza dei pagamenti delle rate | semestrale |
| Tipo d’ammortamento | rata costante |
| Tasso annuo nominale (TAN) | 20% |
| Tasso semestrale (TP) | 20%/2 = 10% |
| Tasso annuo effettivo (TAE) | 21% |
| TAEG | 22.498% |
2.2 Tassi d’interesse
Nella prassi delle operazioni di mutuo, intervengono diversi parametri, tra loro correlati, che abbiamo elencato nella tabella qui sopra, di cui chiariamo il senso e le interrelazioni.
Tasso annuo nominale (TAN nella legislazione e nella prassi). Serve per il calcolo delle quote interessi, relative alle varie rate, con la formula degli interessi semplici:
interessi = debito a inizio periodo x TAN x frazione d’anno
In questo contratto, con riferimento al primo periodo, si ha TAN = 20%
interessi = 1000 x 20% x 1/2 = 100
come controllabile sul piano d’ammortamento allegato.
Tasso periodale (TP). Si riottiene lo stesso risultato del calcolo precedente:
interessi = debito a inizio periodo x TP
infatti il TP equivalente è
20%/2 = 10%
e
interessi = 1000 x 10% = 100
Tasso annuo effettivo (TAE). È un tasso naturale se si parte dalle rate ed è legato al TP dalla relazione:
TAE = (1 + TP) numero annuo di periodi – 1
Nel caso di questo contratto, visto che il numero annuo di periodi è 2, troviamo:
TAE = (1 + 10%)2 – 1 = 21%
Il TAE gode d’un’importante proprietà: il valore scontato composto complessivo a TAE delle rate coincide con l’ammontare mutuato. Ciò spiega quanto prima scritto ossia che nel caso di mutui con rata costante l’uso di tale parametro è il più naturale.
Nel caso di questo contratto, il TAE riesce 21%, il valore delle rate a sconto composto con tasso 21% coincide con l’ammontare mutuato.
La rata semestrale è pari a:
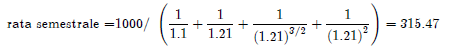
e il valore scontato composto delle rate risulta:
| 315.47 | 315.47 | 315.47 | 315.47 | |||||
| ______ | + | ______ | + | ______ | + | ______ | = | 1000 |
| 1.1 | 1.21 | (1.21)3/2 | (1.21)2 |
che coincide con l’ammontare mutuato.
Tasso annuo effettivo globale (TAEG nella legislazione dagli anni Novanta). Esso nasce nel quadro della normativa di trasparenza; è quel tasso per il quale valga la menzionata importante proprietà del TAE, ma includendo nel calcolo anche ulteriori oneri caricati al mutuatario.
Nel caso di questo contratto, includendo i seguenti oneri accessori:
- 5 euro di spese postali per ogni rata;
- 1% di provvigione d’incasso.
L’effetto pratico di questi oneri è che l’ammontare delle rate diviene:
315.47 + 1.5 + 0.01 x 315.47 = 320.12
l’equazione che determina il TAEG (x) è:
![]()
Esso risulta 22.498%.
2.3 Piano d’ammortamento
La visione complessiva del mutuo oggetto di questo contratto emerge dal piano d’ammortamento.
| tempo | Debito | Rata | Capitale | Interessi |
| 0 | 1000 | – | – | – |
| 0.5 | 1000 – 215.47 = 784. 53 | 315.47 | 215.47 | 100 |
| 1 | 784.53 – 237.02 = 547. 51 | 315.47 | 315.47 – 78. 453 = 237. 02 | 784.53 x 0.1 = 78. 453 |
| 1.5 | 547. 51 – 260. 72 = 286. 79 | 315.47 | 315.47 – 54. 751 = 260. 72 | 547. 51 x 0.1 = 54. 751 |
| 2 | 286. 79 – 286.79 = 0 | 315.47 | 315.47 – 28.679 = 286. 79 | 286.79 x 0.1 = 28. 679 |
2.4 Preammortamento
Qualora il contratto prevedesse un periodo di preammortamento si debbono aggiungere righe, relative a tale periodo. Se, per esempio, esso fosse d’un anno e mezzo (ossia tre semestri), il piano avrebbe 3 righe in più e diverrebbe:
| tempo | Debito | Rata | Capitale | Interessi |
| 0 | 1000 | – | – | – |
| 0.5 | 1000 | 100 | – | 100 |
| 1 | 1000 | 100 | – | 100 |
| 1.5 | 1000 | 100 | – | 100 |
| 2 | 1000 – 215.47 = 784. 53 | 315.47 | 215.47 | 100 |
| 2.5 | 784.53 – 237.02 = 547. 51 | 315.47 | 315.47 – 78. 453 = 237. 02 | 784.53 x 0.1 = 78. 453 |
| 3 | 547. 51 – 260. 72 = 286. 79 | 315.47 | 315.47 – 54. 751 = 260. 72 | 547. 51 x 0.1 = 54. 751 |
| 3.5 | 286. 79 – 286.79 = 0 | 315.47 | 315.47 – 28.679 = 286. 79 | 286.79 x 0.1 = 28. 679 |
2.5 Il caso di rate non costanti
Gran parte del contenzioso in tema d’ammortamento e d’anatocismo riguarda il caso del c.d. ammortamento francese, il cui nome italiano corretto è ammortamento progressivo.
Tale procedura d’ammortamento è caratterizzata dal fatto che le rate sono costanti nel tempo.
Il c.d. ammortamento italiano, caratterizzato dalla costanza nel tempo delle quote di capitale è meno usato, essenzialmente perché le rate sono decrescenti nel tempo e per chi si finanzi per un’attività produttiva, l’estinzione del debito risulta più onerosa proprio quando l’attività produttiva finanziata può liberare con maggiore difficoltà risorse per il servizio del debito. Non è necessario neanche un corso di Economia 1, ma basta un corso di Economia 0 per capire.
Abbiamo osservato uno strano silenzio sul fatto che nel caso italiano non si sia mai concentrato l’interesse di chi ritiene anatocistico il francese, basandosi sul fatto che, in esso, il valore scontato in regime composto delle rate coincide col debito e ciò proverebbe la natura anatocistica dell’ammortamento progressivo. La radice del malinteso è patentemente la solita: quando s’attualizzano le rate in regime composto, non si calcolano interessi. Essi sono separatamente calcolati in maniera non anatocistica, con la solita metodologia, che abbiamo visto sopra.
Sotto l’ovvia ipotesi d’intertempi non superiori all’anno, gli interessi sono semplici a TAN[5]5.
Quanto abbiamo visto fin qui in tema di rata costante, funziona analoga- mente, anche in casi di rate non costanti.
Esibiamo un esempio, simile a quanto visto prima. Indichiamo qui sotto, al solito, i parametri rilevanti.
| Ammontare del finanziamento | 1000 |
| Durata del finanziamento (anni) | 2 |
| Cadenza dei pagamenti delle rate | semestrale |
| Tipo d’ammortamento | italiano |
| Tasso annuo nominale (TAN) | 20% |
| Tasso semestrale (TP) | 20%/2 = 10% |
| Tasso annuo effettivo (TAE) | 21% |
| TAEG | 22.57% |
In questo caso le quote di capitale sono costanti e pari a:
| 1000 | |||
| ______ | = | 250 | |
| 4 |
I debiti residui alle scadenze 0, 0.5, 1, 1.5, 2 risultano:
| Scadenza | Debito residuo |
| 0 | 1000 |
| 0.5 | 750 |
| 1 | 500 |
| 1.5 | 250 |
| 2 | 0 |
Le quote d’interesse e le rate riescono:
| Scadenza | Quota interessi | Rata |
| 0.5 | 1000 x 10% = 100 | 350 |
| 1 | 750 x 10% = 75 | 325 |
| 1.5 | 500 x 10% = 50 | 300 |
| 2 | 250 x 10% = 25 | 275 |
Cominciamo con l’osservare che la variabilità delle rate non impedisce la condizione che ben conosciamo: il valore scontato delle rate, non considerando gli oneri accessori, calcolato a TP, riesce uguale all’ammontare mutuato:
350/1.1 + 325/1.12 + 300/1.13 + 275/1.14 = 1000
Tasso annuo effettivo globale (TAEG nella legislazione dagli anni Novanta). Esso nasce nel quadro della normativa di trasparenza del credito al consumo ed è mutuato (nella struttura di fondo) nella normativa antiusura: è quel tasso per il quale valga la menzionata importante proprietà del TAE, ma includendo nel calcolo anche ulteriori oneri caricati al mutuatario.
Nel caso di questo contratto, includendo i seguenti oneri accessori:
- 5 euro di spese postali per ogni rata;
- 1% di provvigione d’incasso.
L’effetto pratico di questi oneri è che l’ammontare delle rate, oneri inclusi diviene:
| Scadenza | Oneri | Rata con oneri |
| 0.5 | 350 + 1.5 + 0.01 X 350 | 355 |
| 1 | 325 + 1.5 + 0.01 X 325 | 329.75 |
| 1.5 | 300 + 1.5 + 0.01 X 300 | 304.5 |
| 2 | 275 + 1.5 + 0.01 X 275 | 279.25 |
L’equazione in x che determina il TAEG in questo caso risulta:
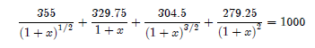
Con soluzione x = 0.225 65 = 22.57%.
La costruzione del piano d’ammortamento può farsi con gli elementi sopra individuati.
Come si può constatare, cambiando la struttura del processo di rimborso, non è cambiato nulla negli indici finanziari, salvo che nel TAEG. La questione è inavvertita nella letteratura italiana, ma è d’interesse provato nella letteratura finanziaria internazionale[6]6.
3. Comuni contestazioni e loro infondatezza
3.1 Comuni contestazioni
Nel contenzioso bancario più recente sono ricorrenti contestazioni anche tecniche sulla legittimità delle clausole dei più comuni contratti di finanziamento che prevedono l’applicazione dell’ammortamento alla francese.
Il Leitmotiv che ricorre è legato al fatto che il modo più semplice per costruire tali piani d’ammortamento fa ricorso al regime dell’interesse composto.
Queste le principali contestazioni.
- Poiché il regime d’interesse usato per costruire il piano di ammortamento alla francese è il composto, si sostiene che tale metodo di ammortamento comporti automaticamente anatocismo.
- Qualora l’applicazione del regime d’interesse composto non venga esplicitata contrattualmente, si invoca l’indeterminatezza delle condizioni dei contratti bancari e/o la violazione della normativa di trasparenza dei contratti bancari.
- Considerato che, nei periodi superiori all’anno, il regime di interesse composto è più oneroso del semplice, si sostiene la necessità di dover determinare un differenziale di regime d’interesse che assume rilievo ai fini delle verifiche di non-usurarietà dei tassi di interesse (ovvero, detto differenziale viene incluso nel calcolo del Tasso Effettivo Globale o T.E.G. relativo al finanziamento specifico da confrontarsi con le soglie di usura).
- Infine, si sostiene che l’ammortamento alla francese vìola la disciplina dell’imputazione dei pagamenti (articoli 1193 ss. del codice civile), che vorrebbe, secondo questa tesi, che i pagamenti siano da imputarsi prima al capitale e solo dopo agli interessi, se il capitale non è ancora interamente scaduto.
3.2 Il regime composto implica anatocismo?
Il regime di interesse composto non comporta di per sé alcun effetto anatocistico, come ampiamente dimostrato dal Rapporto Scientifico AMASES[7]. In particolare un piano d’ammortamento può essere ottenuto attraverso la capitalizzazione composta ed equivalentemente la semplice[8]. È evidentemente sbagliato affermare che un piano d’ammortamento porta con sé un regime di capitalizzazione[9], che dovrebbe essere formalmente dichiarato.
Aggiungiamo un semplice esempio della fallacia dell’idea:
regime composto implica anatocismo
Esempio. Si prestano 100 euro al 10% per due anni. Alla fine del primo anno il mutuatario paga solo gli interessi, d’ammontare 10. Alla fine del secondo anno paga interessi e restituisce il capitale cioè 10 + 100 = 110. È ovvio che non c’è calcolo di interessi su interessi. Il valore scontato a sconto composto dei due pagamenti è:
| 10 | 110 | |||
| ______ | + | ______ | = | 100 |
| 1 + 10% | (1 + 10%)2 |
Nonostante s’usi il regime composto, l’anatocismo non c’è!
Osservazione ed esempio istruttivo. A riprova dell’attenzione con cui queste questioni vanno trattate, sottolineiamo che se gli interessi fossero calcolati in regime composto con il tasso annuo TAE (cfr. sopra 2.1), gli interessi ottenuti sarebbero gli stessi nel caso di rate annue e addirittura minori nel caso di rendite frazionate.
Ecco un esempio numerico di supporto al caso frazionato. Supponiamo che il debito su cui calcolare gli interessi sia 1000 euro e che il TAE sia 10%. La cadenza delle rate sia semestrale. Gli interessi semplici sul semestre:
1000 x 10% x 1/2 = 50
Gl’interessi composti sono:
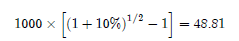
Si sente frequentemente asserire che gli interessi composti su archi di tempo ampi conducono a crescite abnormi: che è vero, mentre non si sente mai asserire che su archi di tempo inferiori all’anno gli interessi composti sono minori dei semplici. Nella costruzione di gran parte dei piani d’ammortamento, quando si calcolano interessi, il periodo praticamente sempre non supera l’anno.
3.3 La mancata esplicitazione del regime di calcolo implica indeterminatezza del contratto? Ammortamento e trasparenza
La mancata esplicitazione in contratto del regime di calcolo composto non implica indeterminabilità (ai dell’articolo 1346 del codice civile) degli interessi dovuti in ciascuna rata.
Come risulta in ispecie dalle sottosezioni 2.1-2.3, parametri necessari a permettere l’individuazione di una sola quantità di interessi rata per rata sono anche solo, per esempio: l’importo totale degli interessi dovuti per tutta la durata del finanziamento, il tasso d’interesse nominale, il numero delle rate, la precisazione che queste sono costanti, l’importo di ciascuna rata. Fissati questi parametri si dà solo una ripartizione dell’importo totale degli interessi tra le rate, solo una possibilità della distinta quota d’interessi compresa in ciascuna rata.
D’altro canto – si aggiunge ad abundantiam – l’associazione ammortamento francese-interesse composto è, delle due possibili, la più comoda[10]. È quindi ragionevole ritenere che il regime naturale d’interesse in cui è normalmente effettuata la costruzione d’un piano d’ammortamento alla francese è il composto. Tuttavia, un piano alla francese può essere costruito partendo dalla fissazione delle quote di capitale appropriatamente, in modo che la loro somma sia uguale al debito da estinguere e che riescano adeguatamente crescenti in modo che la somma capitale + interessi sia la stessa ad ogni scadenza. Il calcolo di tali interessi avviene in regime d’interesse semplice con tasso il TAN. Ma è solo una diffusa leggenda metropolitana quella secondo cui gli interessi composti sono sempre maggiori dei semplici. È matematicamente falso! Lo abbiamo visto sopra, in chiusura dell’ultima sottosezione.
Quanto all’obiettivo della trasparenza, in fondo, l’indicazione del regime finanziario è inutile e fuorviante. Il metodo di calcolo risulta infatti incomprensibile al cliente medio e, quando invece fosse per il cliente comprensibile, sarebbe anche per esso agevolmente ritraibile dai dati sopra indicati ai fini della determinabilità degli interessi.
Ciò che può essere sufficiente al cliente medio, in aggiunta ai dati sopra indicati, per la agevole comprensione del fenomeno e valutazione della convenienza del contratto, è che il contratto spieghi che, costante la rata, la quota interessi diminuisce, mentre s’incrementa la quota capitale e che accompagni tale spiegazione con un esempio, ovvero, più semplicemente, con il piano d’ammortamento, con ciascuna rata suddivisa in quota d’interesse e quota di capitale[11].
3.4 Differenziale d’interesse e soglia d’usura
Non è poi condivisibile la tesi secondo la quale dovrebbe essere determinato un differenziale di regime d’interesse da includersi nel T.E.G. Il nostro punto di vista è stato già stato accolto in giurisprudenza. Cfr., per esempio, Sentenza Trib. Milano n. 3556/2023. Il passaggio d’interesse ai fini dell’usura è riportato alla p. 7 della sentenza e conferma la validità del principio di omo- geneità/simmetria (cfr. Cass., Sez. Un., 20 giugno 2018, n. 16303 e Cass., Sez. Un., 18 settembre 2020, n. 19597), secondo il quale il tasso effettivo relativo al singolo rapporto deve essere determinato tramite la medesima metodologia assunta ai fini dell’individuazione dei limiti di legge, ovvero delle soglie di usura, con riferimento sia alla formula utilizzata sia ai criteri di imputazione degli oneri rilevanti dai quali devono necessariamente essere esclusi elementi di costo unilateralmente determinati e/o non previsti dalle apposite Istruzioni di Banca d’Italia: “Parte attrice ha allegato che il TEG del contratto di leasing sarebbe usurario dopo aver considerato, quali costi ed oneri del contratto di leasing, una serie di oneri unilateralmente determinati (come “l’onere implicito di differenziale di regime” del valore di € 925.481,10), così alterando il principio di simmetria che deve governare il raffronto tra la soglia usura rilevata trimestralmente con decreto del Ministero del Tesoro ed il TEG del singolo contratto. In altre parole, l’inserimento arbitrario di costi unilateralmente determinati dalla parte tra quelli considerati per il calcolo del TEG, incide sulla fondatezza della deduzione in punto di superamento della soglia usura, poiché non può essere considerato logicamente e scientificamente attendibile il raffronto con il tasso soglia usura determinato conteggiando alcuni oneri e costi, ossia quelli indicati nelle Istruzioni di Vigilanza di Banca d’Italia ed un TEG calcolato considerandone altri, poiché così verrebbero confrontate grandezze tra loro eterogenee. La necessità di rispettare il principio di simmetria ai fini della verifica dell’usurarietà dei tassi di interesse è, del resto, stato autorevolmente sostenuto dalla Cassazione a Sezioni Unite quando si è pronunciata in materia di usurarietà degli interessi di mora (cfr. Cass. Sez. Unite n. 19597/2020), e non si ha ragione di discostarsi da tale orientamento, con la conseguenza che l’inattendibilità dei calcoli compiuti da parte attrice al fine di allegare l’usurarietà del tasso leasing convenzionale dimostra l’infondatezza del fatto allegato e comporta il rigetto di tutte le domande (dichiarative e di condanna), fondate su tale allegazione”.
Le ragioni fondamentali della nostra posizione possono essere così riassunte.
- La formula del T.E.G. è stabilita dalle apposite Istruzioni di Banca d’Italia[12], che specificano altresì quali sono gli oneri rilevanti da includere ai fini del calcolo del tasso e non prevedono l’inclusione di un “differenziale di regime”.
- Il T.E.G. (in analogia col T.A.E.G.) è nient’altro che il tasso interno (popolare come “tasso interno di rendimento, siglato T.I.R.” in regime composto). Esso non dipende dalla data iniziale, finale, qualsiasi altra alla quale riferire l’uguaglianza di valore delle prestazioni corrispettive, Non è ragionevole usare lo stesso approccio in regime semplice perché, in tal caso, il tasso risulta dipendere anche da tale data, che può scegliersi ad arbitrio e che risulta pertanto arbitrario.
- L’inclusione di detto differenziale di regime nel conteggio comporterebbe una evidente duplicazione di interessi (infatti, gli interessi eventualmente derivanti dall’applicazione del regime composto sono già considerati per intero ai fini del calcolo del T.E.G.).
Per tali ragioni il tasso calcolato includendo il differenziale di regime d’interesse e in base ad una formula in regime d’interesse semplice, non può essere confrontato con le soglie di usura poiché determinato in modo non omogeneo con le stesse[13].
3.5 Ammortamento, determinatezza e trasparenza
A nostro modo di vedere i due obiettivi (della determinatezza e della trasparenza), fermo quanto rilevato in 3.3, si possono raggiungere, nella prassi contrattuale, inserendo dapprima nel contratto quanto abbiamo visto sopra in 2.1:
| Ammontare del finanziamento |
| Durata del finanziamento (anni) |
| Cadenza dei pagamenti delle rate |
| Tipo d’ammortamento[14] |
| Tasso annuo nominale (TAN) |
| Tasso periodale (TP) |
| Tasso annuo effettivo (TAE)[15] |
| TAEG |
L’indicazione del regime finanziario è inutile e fuorviante. Abbiamo visto che un piano d’ammortamento si può costruire usando congiuntamente il regime composto e il semplice.
Allegheremmo alche il piano d’ammortamento, con ciascuna rata suddivisa in quota d’interesse e quota di capitale[16]: il totale degli interessi è la somma della colonna delle quote interessi.
La trasparenza, però, dipende crucialmente dalle competenze del lato mutuatario. Sebbene nessuna norma lo preveda, l’obiettivo di massima trasparenza potrebbe raggiungersi illustrando la costruzione della quota d’interesse in una rata (per es., la prima) secondo lo schema visto in apertura di 2.2. Naturalmente i calcoli dovrebbero essere esposti usando i numeri dello specifico contratto. La sua assenza non potrebbe comunque essere addebitata al mutuante in tema di trasparenza.
3.6 Ammortamento e imputazione dei pagamenti
Neppure è corretta, infine, la contestazione che l’ammortamento alla francese contrasta con la disciplina dell’imputazione dei pagamenti in quanto questa vieterebbe al creditore di imputare il pagamento agli interessi prima che al capitale non ancora scaduto.
Perché nessuna norma vieta una clausola di tal contenuto.
Anzi, il debitore proprio non potrebbe imputare, senza il consenso del creditore, il pagamento prima al capitale non ancora scaduto e poi agli interessi (a meno che, forse, il debito per capitale non sia ancora liquido) (art. 1194 c.c.)[17]. Come comprovano anche gli articoli 1816 e 1820 del codice civile: la prima norma infatti stabilisce che il mutuatario non può rimborsare il capitale prima della scadenza (se non in uno con gli interessi maturati e maturandi sino alla scadenza); la seconda, nello stabilire che il mutuante possa domandare la risoluzione del contratto anche solo per il mancato pagamento degli interessi, alla scadenza, postula che vi possa essere una parte di capitale non ancora scaduta ed esserci invece interessi già scaduti, il cui mancato pagamento legittima il mutuante ad esigere, a seguito della risoluzione del contratto, l’immediata restituzione dell’intero capitale non ancora rimborsato.
[1] Questo schema di restituzione, comunemente detto “alla francese” è popolare, per la comodità di generare rate costanti. La formula c.d. “all’italiana” genera pagamenti decrescenti nel tempo, proprietà evidentemente non congeniale al caso di mutui destinati a sostenere attività produttive.
[2] Questo avviene se esse sono in progressione geometrica con ragione 1+TP. Ci si convince di questo in quattro e quattr’otto. Lo facciamo sul caso di ammortamento annuo per semplicità. Funziona anche nel caso frazionario.
Si parte dall’uguaglianza desiderata tra le rate a due scadenze consecutive, t e t + 1:
Ct + It = Ct+l + It+l
dove C, I stanno per quota di capitale e quota d’interesse e gl’indici corrispondono alle due scadenze consecutive. Se ne trae:
Ct+l = Ct + It – It+l
Se i è il tasso effettivo e con D indichiamo i debiti residui, sostituendo si trova:
Ct+l = Ct + iDt-l – iDt
Poiché si ha:
Dt-l – Dt = Ct
Ct+l = Ct + iCt = Ct (1 + i)
Quanto trovato prova che, se si vuole la costanza delle rate, le quote di capitale debbono essere scomposte in capitale e interesse esattamente nel modo indicato. Se si scegliessero quote interessi e quote di capitale in modo diverso s’uscirebbe dal francese.
[3] Per molte interessanti osservazioni in tema suggeriamo, per esempio, F. Cacciafesta, Un’ordinanza fondata su un equivoco (l’ammortamento francese secondo il Tribunale di Salerno), in www.ilcaso.it, 2023.
[4] Per un riscontro, suggeriamo: F. Pressacco, F. Beccacece, F. Cacciafesta, G. Favero, P. Fersini, M. Li Calzi, F. Nardini, L. Peccati, L. Ziani, Rapporto scientifico n. 2022/01 dell’AMASES, Anatocismo nei piani di ammortamento standardizzati tradizionali, Udine, 2022. È possibile scaricare il fascicolo gratuitamente dal sito AMASES.
[5] Sarebbero composti se calcolati a TAE, ma, per periodi che non superano l’anno, i composti sono minori dei semplici.
[6] Cfr. C. Battaglio, G. Longo, L. Peccati, Restyling of fees in consumers credit and their optimization, in European Journal of Operational Research, 91, Issue 2, 1996, 330-337.
[7] F. Pressacco, F. Beccacece, F. Cacciafesta, G. Favero, P. Fersini, M. Li Calzi, F. Nardini, L. Peccati, L. Ziani, op. cit..
[8] Per rendersene conto basta riflettere sul fatto che il TAN può essere espresso semplicemente in termini di TAE, via capitalizzazione composta. Naturalmente con l’ampiezza dell’arco di tempo sotteso non supera l’anno, l’anatocismo è escluso, l’interesse semplice supera il composto su tali durate. Ciò nel calcolo degli interessi. Quest’intercambiabilità sparisce quando si costruisce un contratto. L’uso dell’interesse semplice per comparare le prestazioni delle parti è gravemente errato. Il sistema intertemporale di prezzi dell’interesse semplice è internamente incoerente. L’equivalenza di prestazioni con interesse semplice richiede la scelta d’una data (inizio o fine sono le più naturali). Purtroppo contratti equi se valutati all’inizio, non lo sono più con una valutazione finale e viceversa. Poiché il regime composto genera un sistema intertemporale di prezzi internamente coerente, quell’incongruenza sparisce.
Facciamo un esempio. Contro 100€ prestati oggi, a interessi semplici al 10%, la rata annua di restituzione è:
| 100 | ||
| ______ | = | 57.39 |
| 1/1.1 + 1/1.2 |
Infatti:
| 57.39 | 57.39 | |||
| 100 | = | ______ | + | ______ |
| 1.1 | 1.2 |
L’equivalenza in 0 è soddisfatta. Controlliamo se lo è anche in 2. La somma mutuata vale;
100 x 1.2 = 120
mentre la somma dei montanti delle rate:
57.39 x 1.1 + 57.39 = 120.52
e l’equivalenza sparisce. Si lavorasse in regime composto, si scoprirebbe che l’equivalenza che vale a una certa data, vale per ogni altra data.
Riprendiamo l’esempio sopra. L’ammontare mutuato è lo stesso (100), a fronte, il mutuatario pagherà dopo uno e dopo due anni rate uguali. Il TAE è lo stesso (10%) dell’esempio precedente.
La rata costante che consente l’equivalenza in 0 è d’ammontare:
| 100 | ||
| ______ | = | 57.619 |
| 1/1.1 + 1/1.21 |
Spostiamo la data di controllo d’equivalenza due anni più avanti. Il montante della somma prestata è 100 X 1.12 = 121. Il montante delle rate è 50.619 X 1.1 + 50.619 = 121. Scegliessimo qualunque altra data per il check d’equivalenza riscontreremmo sempre l’uguaglianza.
[9] Per motivi che non commentiamo, non viene mai segnalato che se in un piano d’ammortamento all’italiana (quote di capitale costanti), riconosciuto non anatocistico all’unanimità, si calcola il valore attuale delle rate a sconto composto dalla loro scadenza, indietro all’epoca d’erogazione del prestito, s’ottiene proprio tale ammontare. Esattamente come nel caso del francese.
[10] All’italiana, le quote capitali sono costanti e allora, anche potendo usare il composto, nel fare i conti è più comodo viaggiare a interessi semplici, alla francese sono le rate a essere costanti: ecco perché per esso è più comodo usare la capitalizzazione composta.
[11] Al riguardo, amplius, G. Mucciarone, Ammortamento alla francese: meritevolezza e trasparenza, in Banca borsa tit. cred., 2023, I, 6 ss.
[12] Cfr. Banca d’Italia, Istruzioni per la rilevazione dei tassi effettivi globali medi ai sensi della legge sull’usura, aggiornamento 1996 e seguenti, par. C3. Calcolo del TEG.
[13] Cfr. Cass., Sez. Un., 20 giugno 2018, n. 16303 e Cass., Sez. Un., 18 settembre 2020, n. 19597, principio di simmetria/omogeneità.
[14] Il nome tecnico del tipo di ammortamento che ci interessa è progressivo, il nome popolare è francese. Suggeriamo di chiamarlo a rata costante.
[15] Si noti che l’indicazione del TAE e del TAN sono equivalenti. Dall’uno si può ricavare l’altro e viceversa. Basterebbe quindi indicare il TAN. Un dato in più in un documento che può finire nelle mani di non esperti può essere utile.
[16] Prima gli interessi e dopo il capitale in linea con l’art. 1194 cc.
[17] Anche in proposito, amplius, G. Mucciarone, op. cit., 3 ss.


